はじめに


この記事で取り上げる本
この記事の3つの要点
- IUT理論は「未来からやってきた論文」と評されるほど、難解で衝撃を与える内容だった
- IUT理論の理解はなぜ困難で、どのような議論を巻き起こしているのか
- IUT理論の全体像を『宇宙と宇宙をつなぐ数学』に沿って理解する
自己紹介記事



数学界の超重要難問「ABC予想」と、その証明のために生み出された「IUT理論(宇宙際タイヒミュラー理論)」を加藤文元『宇宙と宇宙をつなぐ数学』から学ぶ
この記事の構成

今回の記事では基本的に、『宇宙と宇宙をつなぐ数学 IUT理論の衝撃』をベースにしながら「IUT理論(宇宙際タイヒミュラー理論)」がどんなものなのかについて説明していく。これが本記事のメインである。
またこのIUT理論は常に、「ABC予想」という数学の超難問とセットで語られる。『宇宙と宇宙をつなぐ数学』では、「IUT理論はABC予想解決のためだけの理論ではない」という立場から、「ABC予想」については詳しく触れないと著者が宣言している。そこでこの記事では、『abc予想入門』をベースに「ABC予想」についても触れていく。

「IUT理論」は「ABC予想」を証明するものとして大いに話題になったが、未だに議論の続く理論でもある。
『宇宙と宇宙をつなぐ数学』の刊行時にはまだ、「IUT理論」は査読(正しいかどうか他の数学者がチェックすること)が終わっていなかったが、その後、論文公開から8年が経ってようやくアクセプト(査読誌に掲載)された。

一般的には、査読誌に掲載されると「正しい」と認められるようだが、この「IUT理論」については議論が落ち着いている様子はない。「IUT理論」を巡ってはまだまだ論争が続くことだろう。
そんな「IUT理論」、そして共に話題になる「ABC予想」について、私が理解できている範囲で、可能な限り分かりやすく説明しようと試みるのがこの記事の趣旨である。
(2022年4月20日 追記)
2022年4月10日、NHKスペシャルで「数学者は宇宙をつなげるか? abc予想証明をめぐる数奇な物語」が放送された。「宇宙際タイヒミュラー理論」を一般向けに紹介しようとしたものだ。
「宇宙際タイヒミュラー理論」がどのような流れで生まれたのか、どんなことを目指そうとする理論なのかなど、様々な点から限りなく平易に迫ろうとしている。非常に分かりやすい説明があったので、番組内の説明を踏まえていくつか追記した。

『宇宙と宇宙をつなぐ数学』が読みやすいのは、川上量生が生みの親だから
『宇宙と宇宙をつなぐ数学』(以下『宇宙と宇宙』と表記)は、数学界も困惑するほどの難解な理論が紹介されている割には、文系の人間でも頑張れば読めるぐらいの難易度の本だ(と思う)。なので、この記事で興味を持った方は是非読んでほしいが、そのような易しい本に仕上がっている理由は、本書の成立過程にある。まずその話からしよう。
ニコニコ動画などを手掛けるドワンゴの川上量生が、個人的にスポンサードしている数学イベントがある。そのイベントでのある年の目玉企画として、「IUT理論を一般向けに解説する」というアイデアが出てきた。「IUT理論」は、2012年に京都大学の望月新一教授が自身のHPで発表したものであり、当然正しいかどうかなど誰も分からない代物だった。

しかし、IUT理論によって「ABC予想」を証明したと主張していたし、基本的な発想があまりにぶっ飛んでいて、既存の数学をひっくり返すとんでもない考え方かもしれないとも理解されていた。そして、そんな理論が日本で生まれたのだから、広く知ってもらえる方がいい。そんなわけで解説イベントが企画されることになった。
その「解説者」として白羽の矢が立ったのが、『宇宙と宇宙』の著者である加藤文元だ。彼は、望月教授の盟友であり、しかも、望月教授がIUT理論を作り上げる過程で、毎週のようにマンツーマンで議論(望月氏の考えに対して思ったことを言う、みたいなやりとりだったようだ)をしていた人物でもある。望月教授はあまり人前に姿を現さないことで有名なので(そのことが、IUT理論の受け取られ方にも影響している)、著者は解説者としてうってつけの存在というわけだ。
そんなわけで、「一般向けに講演を行う」ために著者は、分かりやすい説明を苦心して考え、川上量生にプレゼンし、ダメ出しを受ける、というプロセスを何度も繰り返した。そしてそのお陰で、著者によるIUT理論の講演は好評を博し、数学界でも話題になったそうだ。その動画はネットに上がっているので、興味がある方は以下を。

そして、これを一回だけの講演で終わらせるのはもったいない、きちんと書籍化しましょう、ということで、『宇宙と宇宙』が生まれることになったというわけだ。
このような過程で生まれた作品なので、とにかく分かりやすい。もちろん、決して簡単なわけではない。繰り返すが、現在においても数学界で論争が続く理論であり、簡単に理解できる内容であるはずがない。しかし『宇宙と宇宙』では、その本質的な部分を、様々な喩えや例示を駆使して、可能な限りイメージを伝えようと努力している。
現役の数学者がここまで易しく文章が書けることにも驚きだし(数学者に限らないが、専門家の手による文章はどうしても難解になってしまう傾向があると私は思っている)、数学にさほど詳しくない者にも、「IUT理論とはどういうものなのか?」についてざっくりとではあるがイメージを与えてくれるのが素晴らしい。

また本書は、IUT理論そのものについてだけではなく、「IUT理論に対して数学界がどう反応したか」「数学者の仕事とは何か」など、数学を取り巻く話題についても触れられるので、そういう意味でも興味深く読める作品だと言っていいだろう。
「IUT理論(宇宙際タイヒミュラー理論)」に数学界はどう反応したのか
IUT理論は先述した通り、望月教授が自身のHPに論文を載せたことで世に知られることになった。2012年8月30日のことだ。

IUT理論について著者は、
おそらく数学史上に匹敵するものを見出すことが難しいほどの、巨大な影響力をもつイノベーションを起こそうとしているのが、望月教授のIUT理論です
「宇宙と宇宙をつなぐ数学」(加藤文元/KADOKAWA)
と書いているし、エレンバーグという数学者は、

まるで未来からやってきた論文
「宇宙と宇宙をつなぐ数学」(加藤文元/KADOKAWA)
と評したという。

正式発表されたわけではない数学理論がここまで話題になった要因の一つは、やはり「ABC予想」と関係がある。もしIUT理論が正しければ、ABC予想が証明されたことになる。さらに、ABC予想が正しければ「シュピロ予想」や「フライ予想」など数多くの数学の難問が自動的に正しいと認められるそうだ。「ABC予想」を始めとするそれらの未解決問題は数学界において非常に重要だと考えられており、その証明が待望されているからこそ、IUT理論は注目されたのだ。
また、「強いABC予想」と呼ばれるものが正しいと証明されれば、超難問として有名な「フェルマーの最終定理」(1995年に証明された)が10行程度で証明できる、という点も話題になった。数学ファンとすれば、こちらの方が興味深い話かもしれない。


そんなわけで、望月教授の論文は大いに話題になったのだが、しかしすぐに「IUTショック」とでも呼ぶべき状況に陥った。数学者たちが、IUT理論の理解を諦め始めたのだ。
欧米や日本も含めて、世界中の多くの数学者たちにとって、IUT理論の受け止められ方はさまざまですが、多くの場合、次のような印象をもたれている感があります。「IUT理論とは単に新奇な抽象概念が恐ろしく複雑に絡まり合っている理論装置で、その中身はあまりに複雑なので、それをチェックすることは人間業では到底困難である」。したがって、だれもその真偽をチェックできない以上、これ以上まともに請けあってもしょうがないと、多くの数学者たちは考えているようです
「宇宙と宇宙をつなぐ数学」(加藤文元/KADOKAWA)
IUT理論はあまりに「抽象的」「難解」であるため、「人間にはチェック不可能」と思われるほど難しい、と考えられているわけだ。ネットの記事でよく見かける表現としては、「IUT理論が発表された当時、その中身を理解できる人間は数人しかいなかった」というものがある。しかし恐らく、「そもそも理解しようとすること自体を諦めた」という数学者も多かったということだろう。

そう思わせた理由には、私たちにも理解できるもっともな理由もある。
望月教授がHPにアップした論文は500ページ以上にもなるという。これだけでも数学論文としてはかなり長い。しかもこの論文は、望月教授が過去に発表した論文を土台として書かれている。つまり、望月教授の先行論文を読んでいなければ理解できない論文、というわけだ。結局のところ、IUT理論を理解しようとすれば、1000ページ以上もの論文を読む必要がある、ということになる。


これだけでも、その大変さが理解できるだろう。
その上でIUT理論には、それまでには存在しなかった新たな概念が多く含まれており、それゆえ簡単に読み進められる代物ではないのだ。恐らくだが、「別の惑星の言語で書かれたような論文」という感じなのだろう。
そんな理由から、数学者たちはIUT理論を諦めてしまう。

そしてそれは、望月教授の姿勢に原因がある、と非難されることもあるという。というのも望月教授は、「IUT理論を説明してほしい」と声を掛けても、ほとんど出向こうとしないからだ。その態度から多くの数学者は、「彼は自分の理論を説明したくないのだ」と不満を抱いているという。
しかし、望月教授の長年の知己である加藤文元は、こう説明する。仮にIUT理論を大勢の数学者の前で説明しても、恐らくほとんど理解できない。だからこそ望月教授は、少人数でお互いにやり取りを深めながら議論をする、というスタイルにこだわっているのだ、と。理論があまりにも難解であることを理解しているからこそ、適切な手法で広めようとしているのだが、その意図が上手く伝わっていない、というのが著者の受け止め方であるようだ。
IUT理論は、8年の査読期間を経て、京都大学が編集する「PRIMS」に掲載された。しかし、望月教授が「PRIMS」の編集委員長であることから、査読への疑問を表明する声もあるそうだ。編集委員会は「利益相反を避けるために、望月氏を委員会から完全に排除していた」と説明しているが、まだまだ論争は続くのだろう。

(2022年4月20日 追記)
NHKスペシャル「数学者は宇宙をつなげるか? abc予想証明をめぐる数奇な物語」によると、数学者たちにとっての理解のハードルはもう1つあったそうだ。それが「『数学』という学問の根幹」に関わるものだったために、信じがたい反発を食らうことになってしまった。
数学はこれまで、「異なるモノの間に同じ関係を見出す」という基本方針を崩さずにやってきた。例えば、目の前に「リンゴが3つ」と「木の棒に3回巻かれたロープ」が存在するとしよう。「数学的な概念」が存在しない世界では、この2つはただの「異なるモノ」であり共通項などない。しかし、この2つには「3」という同じ関係を見出すことができる。このように、「異なるモノ」を抽象化して「同じ」と見なせる概念を抽出することで「数学」は発展してきたと考えられているのだ。
番組では、有名な数学者アンリ・ポアンカレの、「数学とは異なるものを同じと見なす技術である」という言葉も紹介された。
そしてこの発想にはさらに、「同じと見なしたものは、一貫して同じままだ」という前提が含まれている。つまり、「『同じモノ』が『異なる』なんて状況はあり得ない」というのが数学の大前提なのだ。
しかし望月教授はこの大前提を覆そうとした。つまり、「同じモノを異なると見なす」という発想を取り入れたのだ。

そして多くの数学者が、この考えに異を唱えた。その急先鋒が、現代数学の若手スーパースターと呼ばれるショルツだ。ショルツは、望月教授の「同じモノを異なると見なす」という発想を受け入れなかった。そして、この点を納得させられていないがために、「宇宙際タイヒミュラー理論」は、査読が終了したにも拘わらず異論が出続ける状況に陥ってしまったのである。
『宇宙と宇宙をつなぐ数学』で「ABC予想」をとりたてて扱わない理由
『宇宙と宇宙』にはもちろん、「ABC予想」に関する記述も載っている。しかし「IUT理論がどのようにしてABC予想を証明するのか」という記述はない。何故なら著者は、「ABC予想は、IUT理論に比べたら些末な問題」と考えているからだ。
つまり、「ABC予想を証明するための道具としてのIUT理論」などという低い捉え方ではなく、「数学の概念を一変させるかもしれない理論」としてIUT理論を認識している、ということだ。本書ではその姿勢が貫かれているために、「ABC予想」に関する記述は少ない。

著者は、IUT理論とABC予想の関係について、こんな風にも書いている。
それは、もしかしたら「巨大な遠回り」かもしれませんし、本当は不必要なことだったと、将来明らかになるかもしれません。しかし、従来の数学にはなかった新しい道筋を示す、ということだけでも、IUT理論の人類的な意義があるのだと思います。
「宇宙と宇宙をつなぐ数学」(加藤文元/KADOKAWA)
どういうことか。つまり「IUT理論なんていうどデカい道具を使わなくても、ABC予想を証明できる可能性はあるだろう」という意味だ。IUT理論でABC予想を証明するというのは、「斧で玉ねぎをみじん切りにする」ようなものかもしれない。それはあまりに大げさだと言える。だから将来的に、ABC予想を証明するための「包丁(適切な道具)」が生まれる可能性もある、と示唆しているというわけだ。


ただ仮にそうだとしても、IUT理論の価値が無くなるわけではない。IUT理論はABC予想とは関係なく、数学の概念を一変させるものかもしれないのだ。また、ABC予想はあまりの難解さにどう手をつけていいかさえ分からない難問なのだから、仮にどれだけ遠回りなのだしても、解決の糸口が示されたのならそのことに価値はあるだろう。
さて、そんなわけでここまで、「IUT理論」や「ABC予想」の周辺的な情報について触れてきたが、ようやく「IUT理論」そのものの説明に移ろう。
IUT理論とはどのような理論なのか?
「複数の数学世界」について考える
IUT理論の最も斬新な点は、「複数の数学世界」について考える、という部分だろう。まず、この意味を捉えることが難しい。数学者にしても、「なんでそんなことを考えなければならないんだ?」と疑問を抱いてしまうポイントだ。この点について、『宇宙と宇宙』で紹介されている例ではないが、私なりに説明してみようと思う。

数学には、「ゲーデルの不完全性定理」と呼ばれる有名な証明が存在する。
中身について詳しくは触れないが、この「ゲーデルの不完全性定理」では、「ある数学の体系の中には、その体系においては証明できない命題が必ず存在する」ということが示された。
この意味を説明するために、「人間が生まれつき『温度』を感じ取れない世界」について考えてみよう。「熱い」「冷たい」という感覚もないし、「温度計」や「天気予報の予想気温」なども存在しない世界、というわけだ。
さて、あなたがこのような世界にいるとした場合、「氷が溶ける」という現象は理解不能だろう。「温度」という概念が存在しないのだから、「何もしていないのに固体が勝手に液体に変わる」という風に見えるはずだし、その理由はどれだけ考えても分かるはずがない。

つまり、「温度という概念が存在しない世界」では「氷が溶ける」という現象の説明はつかない(証明はできない)ということになる。

しかし当然だが、「温度という概念が存在する世界」では、「氷が溶ける」という現象は不思議でもなんでもない。
これと同じことが、数学の世界でも起こりうる。

数学という学問は基本的に、「公理」と「推論規則」によって成り立っている。「公理」というのは、「証明無しで『正しい』と定められている主張」のことだ。有名な例で言えば、「ある点からある点に直線が引ける」「ある点から等距離の点をつなぐと円になる」などを挙げることができる。このように、当たり前すぎて「証明する必要がないと考えられている主張」を「公理」と呼ぶ。
そしてその「公理」と「正しい考えの手順(推論規則)」を用いて別の「命題(証明無しでは「正しい」と言えない主張)」を証明していく、というのが数学という学問である。
さて、この「公理」は「証明無しで『正しい』と定める」のだから、どのように決めてもいい。「ある点からある点に直線を引くことができない」という公理を定めてもいいのだ。

私たちが使っている「数学の体系」は、古代ギリシャから連綿と受け継がれてきたものであり、もう固定されてしまっているが、たとえば地球外生命体が存在するとして、彼らが採用している「数学の体系」が私たちのものとはまったく別である可能性はある(というかその可能性の方が高い)。
ゲーデルは「不完全性定理」で、「ある数学の体系の中には、その体系においては証明できない命題が必ず存在する」と示したわけだが、「その体系において証明できない命題」は、別の「数学の体系」においては証明できる可能性がある。つまり、「『私たちが使っている数学の体系』では『証明できないと証明された命題』でも、『地球外生命体が使っている数学の体系』では証明できるかもしれない」というわけだ。
さて、要するにこれが「複数の数学世界」の意味である。私たち地球人が使っている「数学の体系」は1つだが、「数学の体系」というのは「公理」をどう定めるかによって様々な可能性があり得る。そしてそのような「異なる数学世界」について同時に考えよう、というのが「IUT理論」の提案なのだ。

これだけでも、いかに既存の数学からはみ出した異常な主張であるかが理解できるだろう。普通数学者は、「『私たちが使っている数学の体系』で何ができるのか」を考えるものだが、望月教授は「『私たちが使っている数学の体系』だけではない、様々な『数学の体系』について同時に考えよう」と主張しているのだ。常識を逸しているだろう。
しかし、なぜそんなことを考えなければならないのだろうか?
(2022年4月20日 追記)
NHKスペシャル「数学者は宇宙をつなげるか? abc予想証明をめぐる数奇な物語」では、この「複数の数学世界」について、「まったく同じ2つの宇宙(数学世界)だが、異なる点がある」という風に紹介されていた。まさにこの点が、先述した「同じモノを異なると見なす」という部分である。

次の項でもう少し詳しく触れるが、「複数の数学世界」を想定するのは「足し算と掛け算を分離するため」だ。そしてそのために、「宇宙A」と「宇宙B」という“まったく同じ数学世界”を用意し、その2つに関連性があるような状況を作り出すのである。
しかし、「まったく同じ」と言っているにも拘わらず、この2つの「宇宙」は明らかに異なる点がある。この説明に、多くの数学者が困惑するのだ。「まったく同じ」と言っているのなら、これまでの数学の常識に照らして「異なる点など一箇所も存在しない、完璧に同じ状態」でなければならない。しかし、望月教授が主張する「複数の数学世界」は、「まったく同じ」はずなのに違いもあるのだ。自分で書いていて変な文章だと思うが、世界中の数学者も同じように感じたそうである。確かに、シンプルに意味が分からない。
ただ、「異なるモノを同じと見なす」という振る舞いが適切であるならば、その逆がまったく成り立たないなんてこともないはずだと感じる。「異なるモノを同じと見なす」という数学の大前提は、証明されているようなものでは当然なく、数学者にとって「信仰」のような存在なのだと思う。疑う理由が浮かびもしない「信じる対象」というわけだ。
だったら、「同じモノを異なると見なす」という逆の振る舞いも、「それが誤りである」と証明されない限り、「信じる対象」としての可能性は残るのではないかと思う。そう信じたことで生まれた数学が、既存の数学と正しく接続するかどうかは別として、「『同じモノを異なると見なす』という大前提の上に築かれる数学」が存在しても別にいいのではないかと私は感じた。
「足し算」と「掛け算」を分離する

その答えは、「足し算と掛け算を分離するため」だ。これもまた意味不明な主張である。
さて、その説明の前にまず「タイヒミュラー理論」と「IUT理論(宇宙際タイヒミュラー理論)」の関係について触れておこう。
望月教授が「宇宙際タイヒミュラー理論」を発表する以前から、「タイヒミュラー理論」として知られる理論が存在していた。望月教授は、この理論をさらに進化させた、と言っていい。つまり、「『タイヒミュラー理論』を、異なる数学世界間に適応する」という風に拡張したというわけだ。
「宇宙際」という単語は恐らく望月教授の造語だろうが、言葉の使い方としては「国際」に近い。「国際」が「国と国の関係」を指すように、「宇宙際」は「宇宙と宇宙の関係」を指す。望月教授は「1つの数学世界」を「宇宙」に喩え、その関係性について考えた、というわけである。

さてそれではしばらく、「タイヒミュラー理論」の説明をしていこう。この理論の理解のために重要なのが「タイヒミュラー変換」であり、「正則構造を破壊するような変形」のことを指す。
では「正則構造」とは何か。言葉で説明すると「2つの要素が一蓮托生になっているもの」である。つまり、「正則構造を破壊する」というのは、「一蓮托生である2つの要素の一方を固定し、もう一方だけを変形させる」ことを指すわけだ。
これではイメージできないと思うので、具体的に説明していこう。


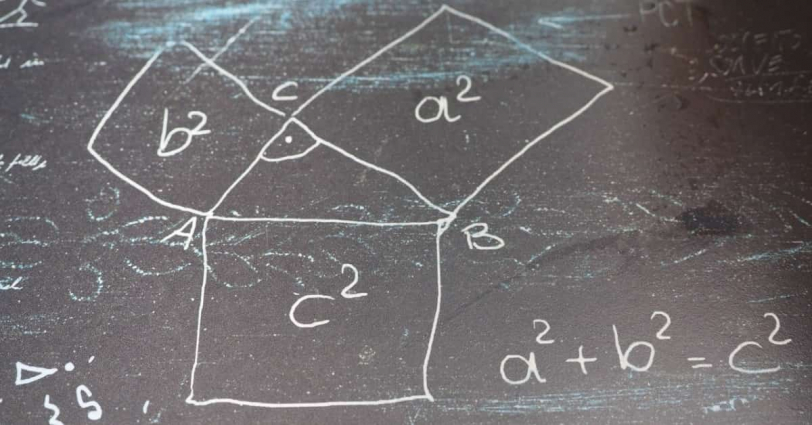
ここでは「正方形」について考える。正方形というのはご存知の通り、「縦と横の長さが同じ図形」だ。つまり、「縦の長さ」と「横の長さ」という2つの要素が一蓮托生になっていると言える。この正方形の例で言えば、「縦の長さ」を変えるなら「横の長さ」も変えなければならない、という状態を「一蓮托生」と呼んでいるわけだ。そうでなければ「正方形」という形を保つことはできない。
そしてこのような関係を「正則構造」と呼ぶ。
「正方形の正則構造を破壊する」というのは、「縦の長さを固定し、横の長さだけを変形させた上で、正方形としての形を保つこと」と表現できる。当たり前だが、そんなことは普通できない。そのような「普通できない」ことをやろうとするのが、「タイヒミュラー変換」というわけだ。
さて、同じことを「足し算」と「掛け算」についても考える。

私には上手く説明できないが、「足し算」と「掛け算」も、正方形の「縦の長さ」と「横の長さ」と同様に密接に結びついており、それは「正則構造」の関係にあるのだという。「足し算」の方を変えれば「掛け算」も変わってしまう、ということだ。
そして望月教授はなんとかして、この「足し算」と「掛け算」の「正則構造」を壊したかった。その動機の1つは、「ABC予想を証明したい」というものだったそうだ。ちゃんとは分からないものの、「『足し算』と『掛け算』の『正則構造』を破壊することができれば、ABC予想の証明の突破口を開けるはずだ」という確信が、望月教授の中にあったというわけである。
彼はどうにかして「足し算」と「掛け算」の「正則構造」を壊す方法を見つけようとした。しかし、2年間考えた結果、彼は「今の数学の体系では不可能だ」と結論する。
普通の数学者であれば、ここで諦めるだろう。しかし望月教授は違った。「正則構造」を破壊できないのは、1つの数学体系だけに囚われているからだ、と考えたのだ。そこで、「複数の数学世界」について考えるという、超絶アクロバティックな思考に行き着くことになる。

このように、「『足し算』と『掛け算』の『正則構造』を破壊したい」という動機が先に存在し、その解決法として「複数の数学世界を想定する」という発想に至ったというわけだ。
「『足し算』と『掛け算』の『正則構造』を破壊する」というイメージ
『宇宙と宇宙』では、「正則構造を壊す」というイメージを伝えるために、2つの例を出している。どちらにも共通していることは、「不可能に思える状況を、複数の世界を想定することでいかにして成り立たせるか」だ。「足し算」と「掛け算」の「正則構造」を破壊することは普通では実現不可能だが、それをどうにか成り立たせる必要がある。その矛盾した状況を、例を使って説明しているというわけだ。
1つ目の例は「ドラマに登場する女優」だ。


Aという女優が、Bという役名の刑事としてドラマに登場しているとする。この場合、「現実の世界ではAという女優」「ドラマの中ではBという刑事」という状況が成立していることになる。つまり、「1人の人物」が「2つの世界を考えることで、違う人物として存在しうる」ということだ。
普通なら「1人の人物が別の人間として存在する」ことは不可能だが、複数の世界の中で考えることで可能になる、というイメージを提示している。
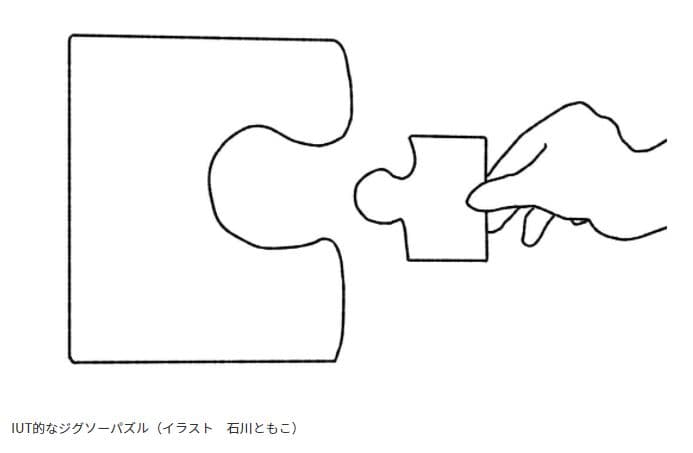
もう1つは、ジグソーパズルを使った例だ。これは言葉では説明が難しいので下の図を見てもらおう

カドブン
2つのジグソーパズルの大きさが違うことが分かるだろう。普通に考えれば、この2つのジグソーパズルははめることができない。しかしどうにかならないだろうか?
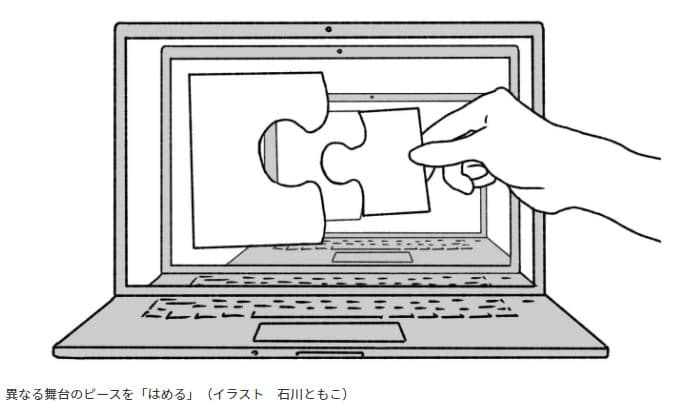
ここで、「入れ子構造」を考える。これも文字だけでは説明が困難なので、以下の図を見てもらおう。手前の画面に映った「凹」と「凸」のような形をしたピースの大きさは違うが、「手前の画面に映った凸」と「奥の画面に映った凹」はピッタリ一致する。
カドブン

このように、「1つの世界で考えていては解決不可能な事柄が、複数の世界を想定することで解決しうる」という状況が、あくまでも例えではあるが示される。
「『足し算』と『掛け算』の『正則構造』を破壊する」というのも、1つの世界だけで考えている場合には絶対に不可能な状況なのだが、「異なる大きさのジグソーパズルが、複数の世界を想定することではまる」のと同じように、複数の数学世界を想定すれば解決可能だと考えるのである。
(2022年4月20日 追記)
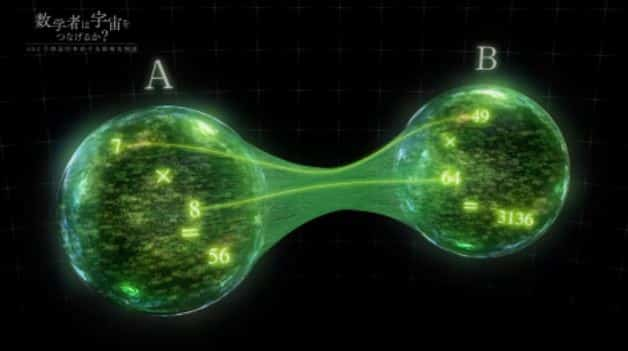
NHKスペシャル「数学者は宇宙をつなげるか? abc予想証明をめぐる数奇な物語」では、「掛け算は成り立つが足し算は成り立たない世界」について非常に分かりやすく説明していた。ここで、「宇宙A」と「宇宙B」が登場する。「『まったく同じ』だが異なる点もある数学世界」だ。
「宇宙A」と「宇宙B」には、「2乗した数字が繋がりを持っている」という関係性がある。「宇宙A」の2と「宇宙B」の4が、「宇宙A」の3と「宇宙B」の9が、「宇宙A」の8と「宇宙B」の64がそれぞれ繋がっているというわけだ。

NHKスペシャル「数学者は宇宙をつなげるか? abc予想証明をめぐる数奇な物語」HP
では、この「2つの数学世界が繋がった宇宙」で「7×8」という掛け算と「7+8」という足し算をしてみよう。
掛け算の場合、「宇宙A」の「7×8=56」という掛け算は、「宇宙B」では「49×64=3136」だ。そして、「宇宙A」の答えである56を2乗すると、「宇宙B」の答えである3136と一致する。「2つの数学世界が繋がった宇宙」でも掛け算は問題なく成立することが分かった。
一方で足し算はどうか。「宇宙A」の「7+8=15」という足し算は、「宇宙B」では「49+64=113」となる。しかし、「宇宙A」の答えである15を2乗すると225なので、「宇宙B」の答えである113と一致しない。つまり、「2つの数学世界が繋がった宇宙」では足し算は成立しないのである。

このような発想をすることで望月教授は、「掛け算は成り立つが足し算は成り立たない世界」を作り出し、「掛け算と足し算の分離」を実現させたのだ。
しかしここに、「同じモノを異なると見なす」という発想が含まれているために議論が絶えないことになる。
問題はこういうことだ。「宇宙A」の4は、「宇宙B」の16と繋がっている。しかし、「宇宙B」の4は、「宇宙A」の2と繋がっているのだ。「宇宙A」と「宇宙B」が”まったく同じ”だというのであれば、同じ4という数字の「繋がり方」も一緒であるべきだろう。しかし、「宇宙A」の4と「宇宙B」の4はそれぞれ別の数字と繋がっているのだ。
このように、「『宇宙A』と『宇宙B』はまったく同じ」と言っておきながら差異が含まれることとなり、現代数学の「タブー」を犯していると批判されているのである。
「複数の数学世界同士の通信」について考える
さて、ここまでで、「複数の数学世界を想定することで、普通には解決不可能な事柄が解決される可能性がある」と理解できた。次に考えることは、「では、その数学世界同士で、どんなやり取りが可能か」ということだ。その「やり取り」のことを、『宇宙と宇宙』では「通信」と呼んでいる。

なぜ「通信(やり取り)」なんてものを考える必要があるのだろうか?
例えば、宇宙のどこかに地球外生命体が存在するとしよう。しかしそれが、1兆光年も先にある星だとしたらどうだろうか。「1兆光年」というのは、「光の速度で進んでも1兆年掛かる距離」のことだ。そんな星に地球外生命体が存在すると分かっても、1往復のやり取りをするのに最低でも2兆年掛かる。まともに「通信(やり取り)」が成立しない存在など、いないのと同じだろう。
数学世界についても同じだ。複数の数学世界を想定したとしても、その数学世界同士で何らかのやり取りが成立しないのなら、存在を仮定する意味などない。干渉せず離れ小島のように存在していても仕方ないので、何らかのやり取りが発生する世界について考えたい、というわけだ。
一方で「正則構造を破壊する」というのは、1つの数学世界では不可能なほど困難なミッションだ。だからこそ、「数学世界同士の通信は容易ではない」という条件も必要となるだろう。何故なら、「通信が容易」である場合、「それぞれの数学世界同士にあまり差が無い」ということになり、複数の数学世界を想定する意味がなくなってしまうからだ。

つまり、「ある程度違いのある数学世界同士で通信が成立する」という条件が満たされる必要があるということだ。

では、そんな条件を満たす「通信」の手段として、どんなものをイメージすればいいだろうか。
ここで、アニメの世界について考えてみよう。私たちは「現実世界」にいて、映画館やスマホで「アニメの世界」を観る。さて、ここからはあくまでもイメージの話として理解してほしい。「現実世界」にいる我々が「アニメの世界」になにか「物質」を届けることは不可能だろう。しかし、「情報」なら届きそうではないだろうか(もちろん届かないのだが、あくまでイメージだ)。「アニメの世界」に「リンゴ」を届けることは無理だが、「リンゴは赤い」という情報を届けることなら、もしかしたら出来そうと思わないだろうか(出来ないのだが、あくまでイメージだ)。

IUT理論でも、同じように発想する。つまり、異なる数学世界に「情報」なら届くのではないか、と考えるのだ。
そしてどんな情報を届けるのかと言えば、「対称性」である。『宇宙と宇宙』には「対称性」に関する易しい説明も載っているが、この記事では省略する。とにかく数学の世界には「対称性」という「情報」が存在するのだと理解してほしい。
そして、別の数学世界に「対称性」を「通信」し、そこで情報を「復元する」ことを考えるのだ。この状況については、「リンゴ」の例で説明してみよう。

今あなたは、「リンゴ」という言葉を使わずに、電話の向こうの相手に「リンゴ」と答えさせるゲームをしているとしよう。あなたは、「丸くて赤い果物」など「リンゴ」に関する性質を相手に伝えることになる。「丸くて赤い果物」では、もしかしたら「さくらんぼ」という答えが返ってくるかもしれない。しかし、「青森県が一番生産量が多い」と言えば、恐らく「リンゴ」という答えが返ってくるだろう。
これは要するに、「物事の性質だけを伝えて、その性質から情報を復元している」ということだ。
IUT理論でも同じことをやろうとしている。「対称性」というのは図形などの「性質」であり(決して図形に限らないが)、この「性質」だけを伝えて、別の数学世界で情報を復元しよう、というのだ。

このようにIUT理論では、「異なる数学世界間の通信」が重要になってくる。
「通信の際の歪み」を定式化する
さて、ここまでくればIUT理論についてはあと少しだ。
今、「異なる数学世界間で、『対称性』を通信する」というところまで来た。そして、その「対称性」から、元の情報を復元したいのだった。

しかし、この「情報の復元」は、100%正確には行われない。
例えば先程説明した電話でのゲームにおいて、相手に「ホーリー」と答えさせたいとしよう。「ホーリー」とは、インドのヒンズー教の祭りの名前だ。しかもそれを、「インド」「ヒンズー教」「祭り」という言葉を使わずに説明しなければならない、とする。
これはかなり難しいだろう。そもそも相手が「ホーリー」を知らない可能性がある。また知っていたとしても、「インド」「ヒンズー教」「祭り」という単語を使えないとすれば、「どこかの国の祭りの名前」というところまでは行き着いても、「ホーリー」にたどり着けるかどうかは分からない。
このように、「物事の性質だけを伝えて、情報を100%完全に復元することは難しい」と理解できるだろう。


IUT理論で想定する「通信」でも同じだ。あるものの「対称性」を「通信」しても、それが100%正確に復元されるとは限らない。というか、「通信」の過程で必ず「ひずみ」が生まれ、正しく復元されない可能性の方が高いのだ。
望月教授は「通信の際の『ひずみ』を定式化できないだろうか」と考えるのである。
その定式化が可能だと主張するのがIUT理論であり、その「ひずみ」を示す不等式が『宇宙と宇宙』にも載っている。そしてこの不等式こそが「ABC予想」の証明の鍵を握るのではないか、という流れになるのだ。

『宇宙と宇宙』ではこのようにしてIUT理論が紹介される。ざっくりとではあるが、この記事でも流れは追えているはずだ。本書を読めば、より詳しく理解できるので、是非手にとってみてほしい。
さてではここから、『宇宙と宇宙』ではあまり触れられてない「ABC予想」について、『abc予想入門』をベースに書いていこう。
ABC予想とは何か?
以下の記事では「ABC予想」と「abc予想」という2つの表記が混在する。私は大文字表記に親しみがあるので基本的に「ABC予想」と書いているが、『abc予想入門』の表記に合わせて小文字になっている箇所もある。

ABC予想が生まれた経緯
ABC予想そのものに触れる前にまず、ABC予想がどのようにして生まれたのかに触れていこう。
以下では「整数」と「多項式」が関わってくる。「整数」については説明は要らないだろうが、「多項式」は説明しておこう。要するに、「複数の項がある式」のことであり、「x+1」や「3a+2b+c」のような式のことを指す。
数学では以前から「整数」と「多項式」には関係があることが知られていた。「整数」の世界で成り立つ理論が「多項式」の世界でも成り立つ、あるいはその逆が成り立つ、ということだ。例えば、「整数」を扱う「数論」という分野で非常に重要とされている未解決問題である「リーマン予想」と「ラングランズ予想」には「多項式」バージョンも存在し、それらは既に証明済みだという。

このような関係があるのだから、「整数」「多項式」それぞれで成り立つ理論をもう一方に当てはめてみたらどうなるだろう、と考えるのは自然なことだろう。
さらに数学の世界には元々、「多項式版ABC予想」と呼ばれるものが存在しており、かなり早い段階で証明されていた。ということは、同じことが「整数」の世界でも成り立つのではないか、と考えたくもなるだろう。

そうやって生まれたのが「ABC予想」である。

ABC予想とは何か?
それでは具体的に、ABC予想の中身に触れていこう。
まず、「実際には成り立たないことが証明された予想」について書こう(『abc予想入門』では「abc予想(願望)」と表記されている)。
「abc予想(願望)」
a,b,cを互いに素な整数でa+b=cを満たすものとすると、
max{|a|,|b|,|c|}<(rad(abc))
が成立する

まず、この数式の意味を説明していこう。
「互いに素」というのは、「共通の約数が1」という意味だ。例えば、「a=2,b=3,c=5」は、「共通の約数が1」なので「互いに素」だ。しかし、「a=4,b=6,c=10」は、2という共通の約数があるので「互いに素」ではない。2で割ってあげることで「a=2,b=3,c=5」となり、「互いに素」と言えるようになる。
【max{|a|,|b|,|c|}】は、「a,b,cの中で、絶対値が一番大きなもの」という意味である。【||】という記号が「絶対値」であり、「マイナスの数でもプラスにして考える」ぐらいに思ってもらえばいい。
具体的に説明しよう(以下の例はすべて、a+b=cという条件を無視している)。

「a=7,b=-25(マイナス25),c=10」とする。この場合、絶対値を考えずに単に数字として一番大きなものを選ぶなら「c=10」だが、絶対値というのは「マイナスをプラスと考える」のだから、この中で絶対値が一番大きな数字は「b=-25(マイナス25)」である。
【rad(abc)】というのは、言葉で説明すると、「a,b,cの素因子の積」という意味になるが、これは具体例がないと理解しにくいだろう。
「a=6,b=12,c=3」とする。それぞれ素因数分解すると、「a=2×3」「b=2×2×3」「c=3」となり、3つの数a,b,cに使われている素因子は「2」と「3」だけということになる。なのでrad(abc)=2×3=6というわけである。
もう1つ例を出そう。「a=7,b=30,c=11」とする。この場合、素因数分解は「a=7」「b=2×3×5」「c=11」となり、使われている素因子は「2」「3」「5」「7」「11」。つまりrad(abc)=2310となるのだ。
これで上述の「abc予想(願望)」の意味は大体理解できるだろうと思う。
しかし、これは成り立たないことが分かっている。そこで数学者は次に、「たぶん成り立つだろう予想」を考えた。これは、一般的には「強いABC予想」として知られており、『abc予想入門』の中では「abc予想(☆)」と表記されている。

「abc予想(☆)」
a,b,cを互いに素な整数でa+b=cを満たすものとすると、
max{|a|,|b|,|c|}<(rad(abc))^2
が成立する
先ほどとの違いは「^2」という部分である。これは「2乗」の表記だ。rad(abc)を2乗するという意味なので、「a=6,b=12,c=3」の場合は(rad(abc))^2=36、「a=7,b=30,c=11」の場合は(rad(abc))^2=5336100ということになる。
さて、これは恐らく正しいだろうと考えられているのだが、まだ証明されていない。そして実は、望月教授がIUT理論によって証明したと主張しているのは、「abc予想(☆)」ではない。望月教授が証明したという予想を「abc予想(望月教授)」と表現すると、
「abc予想(望月教授)」
任意のε>0に対して、ある正の定数K(ε)≧1が存在して、次を満たす:
a,b,cを互いに素な整数でa+b=cを満たすならば、不等式、
max{|a|,|b|,|c|}< K(ε) (rad(abc))^(1+ε)
が成立する
となる。そしてこの「abc予想(望月教授)」こそが、一般的に「ABC予想」として知られているものなのだ。

「^(1+ε)」は先ほど同様、rad(abc)を(1+ε)乗する、という意味になる。何を言っているのかより分かりにくくなったが、「ε=1、K(ε)=1」とすれば、「abc予想(☆)」と同じになることを確認しよう。
さてこのように、「ABC予想」と呼ばれるものにはいくつか種類があり、望月教授が証明したと主張しているのはその内の1つだ、と理解しておくことは重要だ。
「フェルマーの最終定理」との関係性
「ABC予想が証明されたかもしれない」という話が広まった際、「ABC予想が証明されれば、『フェルマーの最終定理』が10行で証明できる」という話も出回った。しかし実際は、仮に「IUT理論によってABC予想が正しいと証明された」のだとしても、「『フェルマーの最終定理』を10行で証明することはできない」のだ。

この辺りの説明をしてこの記事を終えよう。
「ABC予想が証明されれば『フェルマーの最終定理』が10行で証明できる」という時の「ABC予想」は「強いABC予想」と呼ばれるもので、この記事の表記では「abc予想(☆)」である。先程確認したようにこれは、望月教授が証明したと主張する「abc予想(望月教授)」とは別物だ。


そして、「abc予想(望月教授)」が正しいと証明されても、「abc予想(☆)」が正しいかどうかは確定しない。何故か。
先程説明したように、「abc予想(☆)」は、「abc予想(望月教授)」における「ε=1、K(ε)=1」の場合の表現だ。つまり、「abc予想(望月教授)」が正しいとしても、「ε=1の時、K(ε)=1になる」ことが正しいと証明されなければ、「abc予想(☆)」が正しいことにはならない。
そして望月教授は論文の中で、「ε=1の時、K(ε)=1になる」ことを示していない。というか、K(ε)に明確な値を与えていない。
(追記)2021年11月24日に、「K(ε)に明確な値を与え、フェルマーの最終定理を別の形で証明した」という記事が出たのでリンクを貼っておく。

フェルマーの最終定理「おまけで証明」 IUT理論、京大・望月教授

つまり、「abc予想(望月教授)」が正しいと証明されても「abc予想(☆)」が正しいことにはならず、「フェルマーの最終定理」も10行では証明できない、ということになるのである。
「ABC予想が証明されれば、『フェルマーの最終定理』が10行で証明できる」という話はキャッチーであり、ネットで調べるとよく出てくる情報だが、正確に捉えなければ間違えてしまうので注意が必要だ。
そして、『宇宙と宇宙』でも『abc予想入門』でも詳細については触れられていない(もちろん私も理解していない)が、IUT理論が導く不等式を使うと、「abc予想(望月教授)」が正しいことが証明できる、ということになるのである。


最後に

数学界に衝撃や激論、あるいは諦念をもたらした「IUT理論(宇宙際タイヒミュラー理論)」と、それを使うことで正しいと示されるという「ABC予想」について、「なんとなく分かった気になれる作品」だ。『abc予想入門』の方は正直かなり難解で、なかなかお勧めできる作品ではないが、『宇宙と宇宙をつなぐ数学』は、頑張ればなんとかついていける作品だと思うので、是非読んでみてほしい。
数学界を一変させるかもしれない理論が日本で生まれた、というだけで、なんとなくワクワクするではないか。
次にオススメの記事












































コメント