【証明】結城浩「数学ガール」とサイモン・シンから「フェルマーの最終定理」とそのドラマを学ぶ

はじめに

この記事で取り上げる本

この本をガイドにしながら記事を書いていきます

この記事の3つの要点

数学が苦手だという人でも、サイモン・シンの『フェルマーの最終定理』だけは読んでほしい

自己紹介記事

どんな人間がこの記事を書いているのかは、上の自己紹介記事をご覧ください

「フェルマーの最終定理」をきちんと知りたい方に勧めるオススメの2冊、サイモン・シンの『フェルマーの最終定理』と結城浩の『数学ガール』

この記事では、見出しに挙げた2書目を紹介する。「フェルマーの最終定理」そのものにももちろん触れるが、正直、壮大なドラマと重厚な知識の詰まったこの「証明物語」は、簡単には説明できない。是非とも、本を読んでその面白さと衝撃を体感してほしいと思う。

2書目の違いについて書いておこう。どちらも「フェルマーの最終定理」をかなり真正面から扱っている作品だが、ちょっと性質が違う。サイモン・シンの方は、どちらかと言えば「人間ドラマ」に比重が置かれている。一方「数学ガール」では、数学的な記述が重視されている。

どちらも、一般向けの数学書であり、文系の人でも手を出せる作品だ（「数学ガール」の方は、後半に行けば行くほど難易度は上がるが）。「フェルマーの最終定理」とはどんな問題であり、どのような歴史を有し、証明に至る過程でどのような数学的知見が駆使されたのかなどについて詳しく知りたいという方は、是非この2冊を読んでみてほしい。

特に、「数学に興味はあるけれど、全然知識はないし、本1冊読み切れるか自信がない」という方には、サイモン・シンを勧める。サイモン・シンの『フェルマーの最終定理』は、「数学が苦手だという”だけ”の理由で読まないとしたらあまりにももったいない」と感じるほど、読みやすく噛み砕いてくれる。

また、「フェルマーの最終定理」の人間ドラマをメインに取り上げた『哲学的な何か、あと科学とか』に関する記事も書いているので紹介しておこう。

サイモン・シンの『フェルマーの最終定理』は人間ドラマが多めの作品ではあるのだが、決して数学的な記述も逃げていない。「逃げていない」というのは、「どうせわからないだろうから」というような書き方をしない、ということだ。

例えば「フェルマーの最終定理」には、「モジュラー形式」という単語が登場する。私も、これがなんなのか上手く説明できないほど、きちんと数学を学んでいる人でなければ触れる機会がない単語だ。

そして、このような高度は単語が出てくる書籍は大体、数学者が書くことが多いだろうし、そうなると記述が難しくなる。表現は悪いが、書き手が「どうせほとんどの読者には『モジュラー形式』なんて伝わらないだろうなぁ」と考えているような”気がして”しまう記述に出会うこともある。

ただサイモン・シンは、そのような難しい単語や概念の説明からも逃げない。もちろん、その説明が上手くいっているかどうかは読む人次第だと思うが（私は、上手くいっていると思っている）、少なくとも「どうせ伝わらないだろ」という印象にはならない。難しいなりに、ごく一般の人にも伝わるような書き方で説明してくれる。

恐らくそれは、サイモン・シンが数学者ではないからこそだろう。元々はイギリスのBBCで働いており、番組で「フェルマーの最終定理」を取り上げたことで本書を執筆することになった人物だ。サイモン・シンの『フェルマーの最終定理』は、一般向けの数学・科学書の中でも群を抜いた評価がなされているほど評判だ。

騙されたと思って、是非手にとってみてほしい。

「フェルマーの最終定理」とは何か？

この記事では、ざっくりと「フェルマーの最終定理」がどんな問題であるのかに触れていこうと思う。

まず、名前の不思議さの話から始めよう。

「フェルマーの最終定理」は、1995年にアンドリュー・ワイルズによって証明されたが、1600年代にフェルマーという数学者（というか本業は裁判官だったらしいが）が遺して以来、永らく未解決問題だった。

数学において「定理」という言葉は、「証明された」という意味を持つ。しかし「フェルマーの最終定理」は、1995年に証明される以前から「定理」と呼ばれていた。しかも「最終」という単語までついている。「最終」という単語が付く定理・予想は、解決済みであろうが未解決のままだろうが、数学においては「フェルマーの最終定理」ぐらいではないだろうか。

では、なぜそのような呼ばれ方をしているのか。

この説明のためにはまず、フェルマーという人物について触れなければならない。彼は仕事のかたわら趣味で数学の研究を行っていた。そして、当時の一流数学者たちに、「俺はこんな問題を証明したぜ。お前にできるか？」みたいな挑発する手紙を送っていた、らしい（なかなか性格の悪いやつである）。

フェルマーはそんな調子の人物だったから、「どのように証明したのか」を書き残さなかったものも多い。フェルマーの死後、息子が父親の研究などを整理した結果、「父親は証明したって言っているが、その証明が存在しない48個の問題」が明らかになり、これを公表した。

数学者たちは、この48個の問題に取り組んだ。1つ証明するのに数年掛かるような難問もあったそうだが、とにかく数学者の奮闘により、48個の内47個までは「フェルマーが言っている通りすべて正しい」ということが明らかになったのだ。

最後に残ったのが、いわゆる「フェルマーの最終定理」である。「最終」は、「48個の内、最後に残ったもの」という意味なのだ。

そして先述の通り、フェルマーが遺した予想は、48個の内47個すべてが正しかった。だったら恐らく、最後に残ったこの1つも正しいだろう。そういう認識から、証明される以前の段階で「定理」と呼ばれるようになったのだ。

フェルマーの48個の問題は、古代ギリシアの数学者ディオファントスの著作『算術』の余白に書き込まれていたという。『算術』を読みながら、思いついたことをメモしていたのだろう。そして後に「フェルマーの最終定理」と呼ばれることになる余白の書き込みには、有名なこんな言葉が書かれている。

私はこの定理の真に驚くべき証明を持っているが、余白が少なすぎてここには書けない

サイモン・シン『フェルマーの最終定理』

さて、実際に「フェルマーの最終定理」は正しかったのだが、現在では、フェルマー自身は証明できていなかっただろう、と考えられている。何故なら、ワイルズが成した証明には、フェルマーの時代には存在しなかった数学の知見も含まれているからだ。「恐らく証明できたと勘違いしたのだろう」というのが通説のようである。

では、「フェルマーの最終定理」そのものについて書こう。

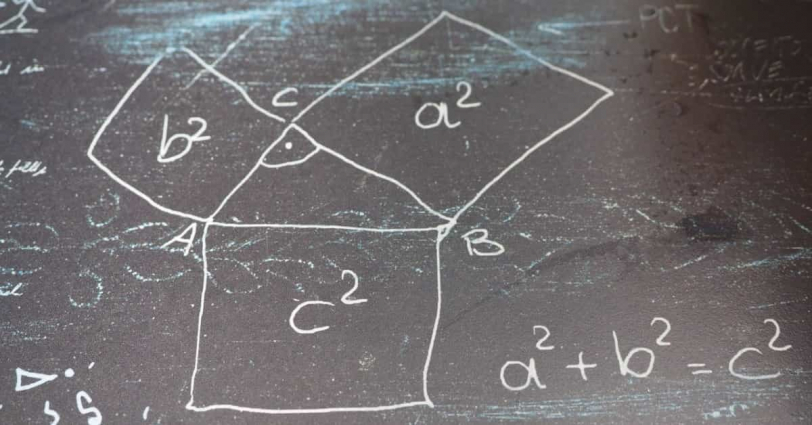
皆さんには、学生時代に習った「ピタゴラスの定理」を思い出してもらいたいと思う。

（xの2乗）+（yの2乗）＝（zの2乗）

というやつである。例えば、「x=3、y=4、z=5」はこの数式を満たす（計算して確かめてみてほしい）。「ピタゴラスの定理」は、上手くx,y,zの数字を選べば、その式を成り立たせる組み合わせを見つけることができる。

では、「2乗」の部分を変えていったらどうだろうか？　つまり、

（xの3乗）＋（yの3乗）＝（zの3乗）
（xの4乗）＋（yの4乗）＝（zの4乗）
（xの5乗）＋（yの5乗）＝（zの5乗）
……

のように、「◯乗」の数字を大きくしていった時に、「ピタゴラスの定理」と同様に数式を成り立たせるx,y,zの組み合わせが存在するだろうか？　ということだ。

そしてフェルマーは、これに「NO」と言った。つまり、「3乗以上の場合は、その式を成り立たせるx,y,zの組み合わせは無い」と主張したのだ。これが「フェルマーの最終定理」である。

数学的にきちんと書くと、以下のようになる。

3以上の自然数nについて、（xのn乗）+（yのn乗）＝（zのn乗）を満たす自然数の組（x,y,z）は存在しない

「フェルマーの最終定理」の特徴は、問題自体は誰でも理解できる、ということだろう。問題そのものは何を言っているのか分かるはずだ。だからこそ、「フェルマーの最終定理」の証明には数多のアマチュア数学者も挑戦したという。

しかし、解くのは相当難しく、だからこそ350年以上に渡って未解決のまま存在し続けた「数学の聖杯」のような存在であり、この証明に関わった人々の物語はそれはそれはドラマティックなのである。

「数学ガール」ではどのように「フェルマーの最終定理」を議論していくか

「数学ガール」は、高校生の男女が数学を通じて成長する青春小説のような体裁を取りながら、数学についてガッツリ学べる作品だ。物語の設定等については以下の記事を読んでほしい。

「数学ガール」では、本の副題が作品全体の「最終到達地点」に設定されており、どう繋がっていくのか分からないような様々な数学的記述が「最終到達地点」の説明として収斂していくという構成になっている。いきなり「フェルマーの最終定理」の話から始めるのではなく、一段一段階段を登るようにして、必要な知識や論理を身に着けながら「最終到達地点」を目指すので、非常に分かりやすいし、置いてけぼりにされずに済む（もちろんそれでも、かなり記述が難しい箇所もあり、ついて行けないと感じる部分もある）。

『数学ガール　フェルマーの最終定理』では、「群」や「体」など、数学の根幹に関係する知識や、「mod」という「ある数で割った『余り』」に注目する考え方、また「原始ピタゴラス数」という本書で初めて知ったような知見まで、様々な事前情報が説明される。

「フェルマーの最終定理」の証明を理解するために必要なステップがきちんと用意されているので、個々の記述を頑張って理解すれば「フェルマーの最終定理」にたどり着ける、という構成が素晴らしい。また、物語形式で進むので、そちらの展開も興味深い。数式がバリバリ出てくるので、文系の人にはハードルが高く感じられるかもしれないが、頑張って食らいつけばそれなり以上に読める作品だと思うので、是非チャレンジしてほしいと思う。

「フェルマーの最終定理」の扱われ方を一変させた「志村＝谷山予想」との関係性

さて、今でこそ「フェルマーの最終定理」は「聖杯」のような扱いになっているし、それを証明したワイルズは賞賛されているのだが、ある時期「フェルマーの最終定理」は「証明しても仕方のない難問」という風に扱われていた。

何故か。

例えば「リーマン予想」と呼ばれる、未だ証明されていない数学の難問がある。この予想の説明はこの記事ではしないが、「リーマン予想」というのは「あらゆる数学者が証明を待ち望んでいるもの」である。これが正しいと証明されなければ研究が進まない、支障を来す、という分野がたくさんある、ということだ。

しかし、かつての「フェルマーの最終定理」はそういう対象ではなかった。非常に有名な問題だし、チャレンジしがいはあるかもしれない。しかし仮に「フェルマーの最終定理」を証明したところで、「フェルマーの最終定理を証明した」という以上の成果はない。つまり、証明されたからといって別の分野に波及するとは思われていなかった、ということだ。

さらに、「フェルマーの最終定理」というのは、長年数多くの数学者の挑戦を跳ね除けてきた難問でもある。もし「フェルマーの最終定理」に手を出せば、一生それにかかりきりになり、数学者としてまったく成果を出せないまま一生が終わる可能性もあるというわけだ。

そんなのは嫌だろう。だから「フェルマーの最終定理」には手を出さないでおこう、と考える者が増えていったのだ。まあ、当然の判断だと思う。

しかしそんなある日、フライという数学者が衝撃的な発表をする。彼は、

もし「志村＝谷山予想」が正しければ、「フェルマーの最終定理」も正しい

と証明したというのだ。

このことが知られるや否や、「フェルマーの最終定理」は再び脚光を浴びることになる。何故なら「志村＝谷山予想」も、多くの数学者からその証明が待ちわびられていた、数学界における非常に重要な難問だったからだ。

今まで「フェルマーの最終定理」を証明しても、「証明したという事実」以外の重要性は存在しないと思われていた。しかし、「志村＝谷山予想を証明すれば、おまけでフェルマーの最終定理もついてくる」と分かった。「志村＝谷山予想」も超絶難問だが、しかしそれにチャレンジすれば「フェルマーの最終定理」もおまけでついてくるならコスパがいいじゃないか。

と考えたかは分からないが、恐らくこのような雰囲気が数学界を取り巻くようになったのだろうと思う。そして数学者は、「志村＝谷山予想」を証明しようと躍起になるのである。

（ここで1つ注意だが、「フェルマーの最終定理が証明されれば、志村＝谷山予想も正しい」という主張は正しくない。あくまでも、「志村＝谷山予想が証明されれば、フェルマーの最終定理も正しい」という主張が正しい、という点を理解しておこう）

では、「志村＝谷山予想」とは一体何なのか？　名前から分かる通り、日本人が生み出した予想である。

これには、「楕円曲線」と「モジュラー形式」という2つのまったく異なる分野が関係する。

「楕円曲線」というのは、古代の数学者から長年研究対象とされてきた、数学における古典的な分野と言える。「フェルマーの最終定理」も、ジャンルとしては「楕円曲線」の問題だと言っていい。一方で「モジュラー形式」というのはかなり新しく、かつ、他の分野との関連性が極めて薄いと考えられている数学である。研究者はいるが、数学全体の中で見れば置き去りにされていると言えるような分野なのだそうだ。

「志村＝谷山予想」は、この「楕円曲線」と「モジュラー形式」を結びつけた。「1つの楕円曲線」に対して「ある特定のモジュラー形式」が対応している、と予想したのだ。

これを例えばアルファベットで考えてみよう。大文字と小文字は1つ1つ対応しており、「A」に対しては「a」、「M」には「m」である。「B」に「b」と「c」が対応するとか、「Q」に対応する小文字が存在しない、みたいなことにはならない。

同じように、「ある楕円曲線」を選べばそれに対応する「モジュラー形式」が1つ存在すると予想した、というわけである。

この予想がなぜ画期的なのかと言えばは、仮に「楕円曲線」の分野で解決できない問題があっても、それを「モジュラー形式」に変換することで解き明かせるかもしれない、と示唆されるからだ。世界中がこのアイデアに熱狂したという。

そして、そんな革命的なアイデアと「フェルマーの最終定理」とがさらに結びつくことになったのだから、数学者が興奮するのも無理はないといえるだろう。

ワイルズの証明と岩澤理論

さて、ここまでくれば準備は整ったといえる。あとは「誰が志村＝谷山予想を証明するか」であり、それを成し遂げた人物がアンドリュー・ワイルズだというわけだ。

ワイルズには、10歳の時に「フェルマーの最終定理」と出会い、「自分がこれを証明するのだ」と意気込んで数学者になったという、これだけで非常にドラマティックな話がある。しかし、やはりというべきか、「フェルマーの最終定理にだけは手を出すな」「証明できなかったら数学者として何の成果も残せないぞ」という忠告を受けることになった。そこで自身の希望は抑えつつ、別の研究を行うことにしたのだ。

彼が研究対象にしたのが、「岩澤理論」と呼ばれる、これもまた日本人数学者が生み出した理論である。彼は「岩澤理論」の専門家として名を馳せることになった。

その後ワイルズは、幼い頃からの夢であった「フェルマーの最終定理」に取り掛かることになるのだが、そのことを妻以外の誰にも言っていなかったという。数学者は普通、自分が今行っている研究について他の数学者とディスカッションをしながら考えを深めていくもので、彼の態度は異例だと捉えられた。他の数学者と接触せず、自分が何を研究しているのかも話さず、ひたすら屋根裏で研究を進めたそうだ。

そしてある日、ワイルズは数学者の前でおもむろに自説を披露する。彼が何の研究をしているのかは知られていなかったわけだが、彼の理論が説明されるにつれて、これは「フェルマーの最終定理」のことに違いないとざわつきだし、彼が「証明終了」と告げると興奮に満たされたという。

しかし、ここからがワイルズの苦悩の始まりだった。

数学でも科学でも、発表された論文は他の学者から評価を受ける「査読」というプロセスを経る。そしてこの査読で、ワイルズの証明に致命的な欠陥が見つかったのだ。

ワイルズが埋めきれなかったこの穴を最後に閉じた者が「フェルマーの最終定理を証明した人」として評価される。ワイルズはこれまで、たった一人で研究を続け、証明のほとんどの部分を独力で完成させたのだが、このままでは、最後に穴を塞いだ者が評価されることになってしまう。

ワイルズは追い詰められていた。しかし、何も思いつかない。もうダメか……と諦めかけたその瞬間だったという。

「岩澤理論」が使えるかもしれない、とひらめいた。なんと、彼が専門家として名を馳せた「岩澤理論」が、ワイルズの証明の最後の穴を塞ぐための重要なピースだったのだ。

こうして「フェルマーの最終定理」の証明は完成した。当然ワイルズは世界中から称賛されたが、数学界最高の賞と言われる「フィールズ賞」は受賞できなかった。何故なら「フィールズ賞」には、40歳以下という年齢制限があるからだ。これについては、「数学の重要な仕事は若い頃にしか行えない」とされているからという話を聞いたことがある。しかし、国際数学連盟は「フィールズ賞」を与える代わりにワイルズを特別表彰したという。

こんな風に、最終的な証明を与えたワイルズに限ってみても、これでもかというほどドラマが詰め込まれている。「フェルマーの最終定理」に直接間接に関わったすべての数学者を合わせれば、とても数学の世界の話とは思えないほどの人間模様が描かれる、非常に魅力的な物語なのだ。

最後に

数学というと「無味乾燥」に思われがちだが、真剣に数学と向き合う者たちが織りなすドラマは、決して「無味乾燥」などではない。

サイモン・シンにしても「数学ガール」にしても、数学の難しい記述は出てくるが、分からないところは飛ばせばいい。どれだけの人間が奮闘してきたのかを、是非体感してほしい。

次にオススメの記事

この記事を読んでくれた方にオススメのタグページ

タグ一覧ページへのリンクも貼っておきます