What is IUT Theory and Why Does it Matter for the abc Conjecture?

I wrote this article in Japanese and translated it into English using ChatGPT. I also used ChatGPT to create the English article title. I did my best to correct any translation mistakes, but please let me know if you find any errors. By the way, I did not use ChatGPT when writing the Japanese article. The entire article was written from scratch by me, Saikawa Goto.

Introduction

Movies and books covered in this article

I will write an article about this movie/book

Three takeaways from this article

Kato Fumiharu, a close friend of Professor Mochizuki the proposer of IUT and exchanged weekly communications, breaks down IUT into easy-to-understand terms.

Self-introduction article

Please refer to the self-introduction article above to learn about the person writing this article. Be sure to check out the Kindle book linked below as well.

The quotes in the article were translated using ChatGPT from Japanese books, and are not direct quotes from the foreign language original books, even if they exist.

Composition of This Article

In this article, I will mainly explain what “IUT (Inter-Universal Teichmüller Theory)” is, based on “宇宙と宇宙をつなぐ数学” (hereinafter referred to as “宇宙と宇宙”). This is the main focus of this article.

In addition, the IUT theory is always discussed together with the extremely difficult mathematical problem called the “abc conjecture.” In “宇宙と宇宙,” the author declares that he will not touch upon the “abc conjecture” in detail, taking the position that “IUT is not just a theory to solve the abc conjecture.” Therefore, this article will also touch upon the “abc conjecture” based on the “abc予想入門.”

Although the IUT theory became a big topic as a means to prove the “abc conjecture,” it remains a theory that is still being debated.

When “宇宙と宇宙” was published, the IUT theory had not yet completed peer review (a process in which other mathematicians check whether it is correct), but eight years after its publication, it was finally accepted.

Generally, a paper that undergoes peer review is considered “correct,” but there seems to be no end to the debate surrounding “IUT.” There will likely continue to be controversy surrounding it.

The purpose of this article is to explain, to the best of my understanding, in a clear and understandable way, both the “IUT” and the “abc conjecture” that are often discussed together.

About the Ultra-Important Difficult Problem in the Math World, “ABC Conjecture,” and “IUT (Inter-Universal Teichmüller Theory)” Created to Prove it

“宇宙と宇宙” is Easy to Read Because it was Created by Kawakami Nobuo

“Mathematics that connects 宇宙と宇宙” is a book with a difficulty level that even humanities students can read with some effort, despite introducing theories that are confusing even to the math world. So, if you’re interested, I’d like you to read it, but the reason it turned out to be such an easy-to-read book is because of the process of how it was created. First, let’s start with that story.

There is a math event that Kawakami Nobuo of DWANGO, which is involved with niconico, etc., is personally sponsoring. As one of the highlights of the event one year, the idea of “explaining IUT to the general public” came up. “IUT” was presented by Professor Mochizuki Shinichi of Kyoto University on his own website in 2012, and of course, it was something that no one knew for sure whether it was correct or not.

However, it was claimed that IUT proved the “abc conjecture,” and its basic idea was so unconventional and may even turn the existing mathematics upside down. Since this theory was born in Japan, it is better for many people to know about it.

Thus, an explanatory event was planned, and the author of “宇宙と宇宙,” Kato Fumiharu, was chosen as the “explainer.” He is a close ally of Professor Mochizuki and was a person who had weekly one-on-one discussions with him during the creation of IUT. Since Professor Mochizuki is famous for not appearing in public (which affects how IUT is received), the author is the perfect choice as an explainer.

So, in order to “give a lecture for the general public,” the author worked hard to come up with an easy-to-understand explanation, repeatedly presenting it to Kawakami Nobuo for feedback. Thanks to this process, the author’s lecture on IUT was well received and became a hot topic in the mathematics community. The video of the lecture is available online, so if you’re interested, you can check out the link below.

And so, it would have been a waste to end with just one lecture, so they decided to turn it into a book – and that’s how “宇宙と宇宙” was born.

This work was born through such a process, so it is easy to understand in any case. Of course, it is by no means simple. As I have reiterated, it is a theory that continues to be debated in the mathematical world even today, and it should not be content that can be easily understood. However, in “宇宙と宇宙”, the essential part is conveyed as much as possible using various metaphors and examples to help readers understand the concepts.

It’s amazing that an active mathematician can write such an easy-to-understand sentences (I think that articles written by experts tend to be difficult to understand, not limited to mathematicians), and it is great that even those who are not familiar with mathematics can get a rough idea of “what is IUT?”.

In addition, this book not only deals with IUT itself, but also touches on topics surrounding mathematics, such as “how the mathematical world reacted to IUT” and “what mathematicians usually do”, so it can be said that it is an interesting work to read in that sense.

How did the Mathematical Community React to “IUT (Inter-Universal Teichmüller Theory)”?

As previously mentioned, IUT became known to the world when Professor Mochizuki posted his paper on his own website on August 30, 2012. The author writes the following about IUT:

Professor Mochizuki’s IUT is attempting to create an innovation with a huge impact, which is probably difficult to find something comparable in the history of mathematics.

“宇宙と宇宙をつなぐ数学” (Kato Fumiharu / KADOKAWA)

Also, the mathematician Ellenberg expressed his evaluation as follows.

It’s like a treatise from the future.

“宇宙と宇宙をつなぐ数学” (Kato Fumiharu / KADOKAWA)

One reason why a mathematical theory that has not been formally announced has become such a hot topic is its connection to the “abc conjecture.” If IUT is correct, then it means that the abc conjecture is proven. Furthermore, it seems that if the abc conjecture is correct, many difficult mathematical problems, such as “Szpiro’s conjecture,” are automatically be accepted as correct. These unsolved problems, including the abc conjecture, are considered very important in the world of mathematics, and their proofs are eagerly awaited, which is why IUT has also received attention.

Additionally, if the “strong abc conjecture (I’ll get to this later)” is proven to be correct, the famous and extremely difficult “Fermat’s Last Theorem” (proved in 1995) can be proven in about ten lines, which is also a topic of discussion for math enthusiasts.

So, Professor Mochizuki’s paper caused quite a stir, but soon fell into a situation that could be called “IUT shock.” Mathematicians began to give up on understanding IUT.

For many mathematicians around the world, including those in Europe, the U.S., and Japan, the reception of the IUT varies, but in many cases, IUT is perceived as a “theory device where novel and abstract concepts are incredibly complexly intertwined and difficult to check due to their complexity.” As a result, many mathematicians seem to think that it is useless to take on more serious work since nobody can check its truth or falsity.

“宇宙と宇宙をつなぐ数学” (Kato Fumiharu / KADOKAWA)

It is thought to be too “abstract” and “abstruset” to the extent that it is considered “humanly impossible to check.” In articles on the internet, it is often expressed as “at the time of IUT’s release, there were very few people who could understand its contents.” However, it probably means that many mathematicians “gave up trying to understand it in the first place.”

There are some plausible reasons there that we can understand.

It seems that Professor Mochizuki’s paper, which was posted on his website, is over 500 pages long. That alone makes it quite long for a math paper. Moreover, this paper is written based on previous papers that Professor Mochizuki has published. In other words, it is a paper that cannot be understood without reading Professor Mochizuki’s earlier papers. Ultimately, if they want to understand IUT, they need to read over 1,000 pages of papers.

Just this alone should give you an idea of how difficult it is.

Furthermore, IUT contains many new concepts that did not exist before, making it not an easy read. It is probably like a paper written in the language of another planet.

Due to such reason, mathematicians ended up giving up on IUT.

It’s even said that this is due to Professor Mochizuki’s attitude. Even if asked to explain IUT, Professor Mochizuki hardly tries to do so. From his behavior, many mathematicians are dissatisfied, thinking that “he does not want to explain his theory.”

However, Kato Fumiharu, a longtime friend of Professor Mochizuki, explains as follow: Even if IUT is explained to many mathematicians, they would probably not understand it. That is why Professor Mochizuki insists on a style of discussing and exchanging ideas with a small group of people. He understands that the theory is too difficult to understand, so he is trying to spread it appropriately, but it seems that his intention is not well understood by the other mathematicians.

IUT was published in “PRIMS,” edited by Kyoto University, after an 8-year peer review period. However, since Professor Mochizuki is the editor-in-chief of “PRIMS,” some have expressed doubts about the peer review process. The editorial committee explained that “to avoid conflicts of interest, Mr. Mochizuki was completely excluded from the committee,” but the controversy is likely to continue.

The Reason Why “ABC Conjecture” is Not Featured Prominently in the Book “宇宙と宇宙をつなぐ数学”

Although the book “宇宙と宇宙” contains descriptions related to “abc conjecture,” there is no mention of how “IUT proves the abc conjecture.” This is because the author believes that “abc conjecture is a trivial problem compared to IUT.”

In other words, IUT is not just a tool to prove the abc conjecture, but rather a theory that could completely transform mathematical concepts. This perspective is reflected throughout the book, which is why there are only a few descriptions about the abc conjecture.

The author also writes about the relationship between IUT and the abc conjecture in this way.

That might be a “huge detour,” and we might realize in the future that it was turn out to be something unnecessary. However, even just showing a new path that was not present in traditional mathematics has a significant human significance of IUT, I believe.

“宇宙と宇宙をつなぐ数学(The Mathematics that Connects 宇宙と宇宙)” (Kato Fumiharu / KADOKAWA)

What does it mean? This means that “it may be possible to prove the abc conjecture without using such a grand tool as IUT.” Using IUT to prove the abc conjecture may be said to be like “chopping an onion with an axe,” which would be too exaggerated. It suggests that there may be a “knife (appropriate tool)” in the future to prove the abc conjecture.

However, even if that were the case, IUT still has value. This is because it could change mathematical concepts regardless of the abc conjecture. Moreover, since the abc conjecture is such a difficult problem that it is not even clear how to approach it, if there is any hint of a solution, it is valuable, even if it is a detour.

What is the Theory Behind IUT?

So far, I’ve touched on some peripheral information about “IUT” and “abc conjecture”. Now, let’s finally move on to the explanation of “IUT” itself.

Thinking About “Multiple Math Worlds”

The most innovative aspect of IUT may be its consideration of “multiple math worlds”. However, it would be difficult to grasp its meaning, and even mathematicians may question why it’s necessary. In the book “宇宙と宇宙”, an example is given to explain this point.

In mathematics, there is a famous proof called “Gödel’s incompleteness theorems”.

I won’t go into detail about what’s inside, but first, let’s talk about “Gödel’s incompleteness theorems”. In this famous proof, it is shown that “in a mathematical system, there must be propositions that cannot be proven within the system”.

To explain this, let’s think about a world where humans cannot sense “temperature” by birth. In this world, there is no sense of “hot” or “cold”, and there are no things like “thermometers” or “weather forecasts”.

In such a world, the phenomenon of “ice melting” would be incomprehensible. Since the concept of “temperature” does not exist, it would seem like the solid is changing to liquid on its own, and no matter how much you think about it, it is supposed to be impossible to understand why.

In other words, in a world where the concept of “temperature” does not exist, it is impossible to explain (or prove) the phenomenon of “ice melting”.

Of course, in a world where the concept of “temperature” exists, the phenomenon of “ice melting” is not mysterious at all.

The same thing can happen in the world of mathematics.

Mathematics is a field of study that is essentially composed of “axioms” and “rules of inference.” An “axiom” is a statement that is considered “correct” without proof. Examples of famous axioms include “a straight line can be drawn between any two points” and “connecting points that are equidistant from a point forms a circle.” In this way, axioms are statements that are considered so obvious that they do not need to be proven.

In mathematics, we use these “axioms” and “rules of inference” to prove other statements or propositions that cannot be considered correct without proof.

Since axioms are considered “correct” without proof, we can define in any way. To the extreme, we can define an axiom like “it is impossible to draw a straight line between any two points”(Whether such mathematics makes sense is another matter though).

The “mathematical system” we use has been passed down from ancient Greece and is now fixed. However, if extraterrestrial life exists, it is possible that their “mathematical system” is completely different from ours (in fact, it’s more likely).

Gödel’s “incompleteness theorems” show that there are propositions in a given mathematical system that cannot be proven within that system. However, these unprovable propositions may be proven in another “mathematical system”, which means that even if a proposition is proven unprovable in “our mathematical system,” it may still be provable in the “mathematical system” used by extraterrestrial life.

So, basically this is the meaning of “multiple math worlds”. We humans on Earth use one “mathematical system”, but there are various possibilities for “mathematical system” depending on how we set the “axioms”. And the proposal of “IUT” is to consider such “different mathematical worlds” at the same time.

Just this alone can help you understand how abnormal the claim is that goes beyond existing mathematics. Normally, mathematicians think about “what can be done with ‘mathematical systems’ that we use”, but Professor Mochizuki claims that we should consider not only “mathematical systems that we use” but also various “mathematical systems” at the same time. It might be going against common sense.

But why do we have to think about such a thing?

Separating Addition and Multiplication

The reason for this is to “separate addition and multiplication”. This would be another incomprehensible claim.

Now, before explaining that, let’s talk about the relationship between “Teichmüller Theory” and “IUT (Inter-Universal Teichmüller Theory)”.

Even before Professor Mochizuki announced “Inter-Universal Teichmüller Theory”, there was a theory known as “Teichmüller Theory”. Professor Mochizuki can be said to have further evolved this theory. In other words, he extended “Teichmüller Theory” to apply to different mathematical worlds.

The word “Inter-Universal” is probably a term created by Professor Mochizuki, but it’s used in a way that’s similar to “international.” Just as “international” refers to the relationship between nations, “Inter-Universal” refers to the relationship between universes. Professor Mochizuki likened “one mathematical world” to the “universe” and thought about its relationships.

Now let’s explain the “Teichmüller Theory” for a bit. What’s important for understanding this theory is the “Teichmüller transformation,” which refers to a “deformation that destroys the holomorphic structure.”

So, what is the “holomorphic structure”? It’s “two elements that are inseparable.” In other words, to “destroy the holomorphic structure” means to “fix one of the two inseparable elements and only deform the other.”

I don’t think you can imagine it well, so let me explain it more specifically.

Let’s consider a “square” here. As you know, a square is a “figure with the same length in the height and width.” In other words, we can say that two elements, “height” and “width,” are inseparable. In the case of this square, I call this state where “if you change the height, you must also change the width” as “inseparable”. Otherwise, we cannot maintain the shape called “square.”

This relationship is called a “holomorphic structure.”

To “destroy the holomorphic structure of a square” means to change only the width of the square with the height fixed while keeping its shape. Of course, that is not usually possible. Trying to do something that is not easy like that is what is called a “Teichmüller transformation.”

Now let’s think about the same thing for addition and multiplication.

I can’t explain it well, but just like the “height” and “width” of a square, addition and multiplication are also closely related through the “holomorphic structure.” If yo It means that if you change one of them, the other must also change.

Professor Mochizuki wanted to somehow break the “holomorphic structure” of “addition” and “multiplication.” One of his motivations was to prove the abc conjecture. Even though I don’t fully understand it, Professor Mochizuki believed that if he could break the “holomorphic structure” of “addition” and “multiplication,” it would be a breakthrough for proving the abc conjecture.

He tried to find a way to break the “holomorphic structure” of “addition” and “multiplication,” but after thinking about it for two years, he concluded that it was impossible with the current mathematical system.

A regular mathematician would give up at this point, but not Professor Mochizuki. He thought that the reason why he couldn’t break the “holomorphic structure” was because he was stuck in just one mathematical system. So, he came up with an extremely acrobatic idea of thinking about “multiple math worlds.”

In this way, the motivation to “break the ‘holomorphic structure’ of ‘addition’ and ‘multiplication'” came first, and then the idea of “assuming multiple math worlds” came up as a solution.

“Image of Destroying the ‘Holomorphic Structure’ of ‘Addition’ and ‘Multiplication'”

In “宇宙と宇宙,” two examples are used to convey the image of “destroying the holomorphic structure.” What they have in common is how to make the seemingly impossible situation work by assuming multiple worlds. Destroying the “holomorphic structure” of “addition” and “multiplication” is normally impossible, but it must be made to work somehow. The examples are used to explain this contradictory situation.

The first example is “an actress who appears in a drama.”

Assume there’s an actress named A who appears in a drama as a detective named B. In this case, it means that the situation where “she is an actress named A in the real world” and “she is a detective named B in the drama” is established. In other words, it shows that “one person” can exist as a “different person” by considering “two worlds.”

It means that it’s impossible normally for “one person to exist as a different person,” but by thinking in multiple worlds, it becomes possible.

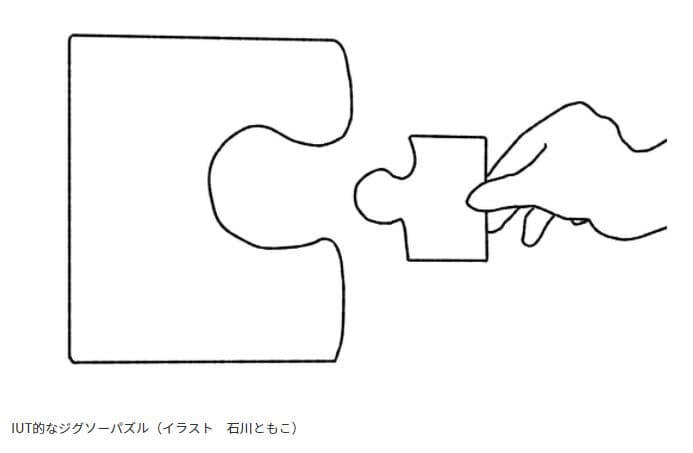
Another example involves using a jigsaw puzzle, which is difficult to explain in words, so please refer to the diagram below.

KADOBUN

You can see that the sizes of the two jigsaw puzzles are different. Normally, you wouldn’t be able to fit these two puzzles together. But is there any way to do it?

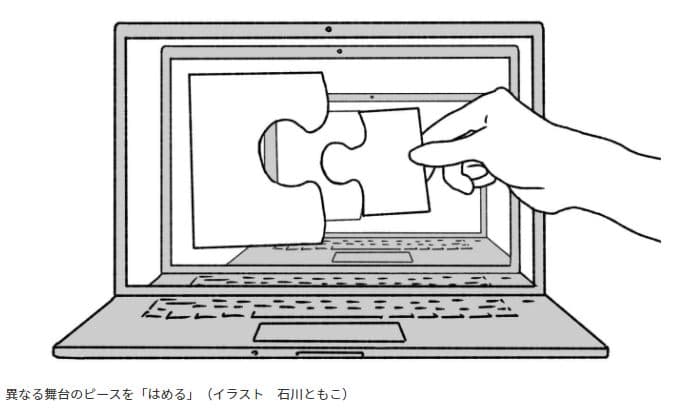
Here, let’s consider a “nested structure.” It is also difficult to explain this with words alone, so please refer to the following diagram. The size of the pieces shaped like “concave” and “convex” that appear on the front screen are different, but the “convex on the front screen” and the “concave on the back screen” fit perfectly.

KADOBUN

In this way, the situation is demonstrated, although it is only an “example,” that issues that are impossible to solve when considering just one world can be resolved by envisioning multiple worlds.

Even though destroying the “holomorphic structure” of “addition” and “multiplication” is an impossible situation when thinking only in one world, just like how different sized puzzle pieces fit together in multiple worlds, he believed that the problem can be solved by assuming the existence of “multiple math worlds”.

Considering Communication Between Multiple Math Worlds

So far, we’ve understood that assuming “multiple math worlds” can potentially solve problems that cannot be solved otherwise. Now we need to think about what kind of communication is possible between these mathematical worlds.

However, why do they need to consider communication?

For example, let’s say there is extraterrestrial life somewhere in the universe. However, what if it exists on a star that is 1 trillion light-years away? “1 trillion light-years” is the distance that takes “1 trillion years” even if we travel at the speed of light. Even if we find out that extraterrestrial life exists on such a star, it would take at least 2 trillion years for one round trip of interaction. It is like saying that there is no such thing as a being that cannot communicate properly.

The same is true for the mathematical worlds. Even if we assume multiple mathematical worlds, if there is no communication among them, there is no point in assuming their existence. It is no use if they exist like isolated islands without interference, so it means that we want to think about worlds where some kind of communication can occur.

On the other hand, destroying a holomorphic structure is an extremely difficult mission in a single mathematical world. Therefore, it is also necessary to have the condition that “communication between multiple math worlds is not easy”. If communication is easy, it means that there is little difference between each math world and the assumption of multiple math worlds loses its meaning.

In other words, it is necessary that communication can take place between math worlds that are different enough.

So, what kind of means can we imagine as a “communication” that satisfies such conditions?

Let’s think about the world of anime for a moment. We are in the “real world” and we watch the “anime world” on a movie screen or a smartphone. Now, from this point on, please understand that I am only talking about images. We cannot deliver any “material” from us in the “real world” to the “anime world.” However, don’t you feel like we can deliver some “information” instead (of course, we cannot, but it’s just an imaginary scenario)? We cannot deliver an apple to the “world of anime,” but don’t you feel like it be possible to deliver the information that “an apple is red” (of course, it’s not possible, but it’s just an imaginary scenario)?

In IUT, we think the same way. That is, we consider whether “information” can be delivered to different mathematical worlds.

Then what kind of information should we deliver? It is “symmetry.” An easy explanation about “symmetry” is also included in “宇宙と宇宙,” but I omit it in this article. Anyway, please understand that there is “information” called “symmetry” in the world of mathematics.

And let’s consider communicating “symmetry” to another mathematical world and “restoring information” there. I’ll explain this situation using the example of an “apple.”

Suppose you are playing a game where you don’t use the word “apple” but make the person on the other end of the phone say “apple.” You will have to convey properties of the apple, such as “round and red fruit,” to the other person. If you say “fruit that is considered the ‘forbidden fruit’ in the Bible,” the answer will likely be “apple.”

In short, this is the idea of “conveying only the properties of things and restoring information from those properties.”

IUT is trying to do the same thing. “Symmetry” is a “property” of shapes and so on (although not limited to shapes), and we are trying to convey only this “property” and restore information in another mathematical world.

In this way, in IUT, it’s important to communicate between different mathematical worlds.

To Formalize the “Distortion During Communication

Now, we’re almost done with understanding IUT.

We’ve reached the point where we want to communicate “symmetry” between different mathematical worlds and restore the original information from that symmetry.

However, this “recovery of information” is not performed with 100% accuracy.

For example, let’s say you want to make the other person answer “Holi” in a game played on the phone that was explained earlier. “Holi” is the name of a festival in Hinduism in India. Moreover, suppose you have to explain it without using the words “India,” “Hinduism,” or “festival.”

This would be quite difficult. First of all, there is a possibility that the other person does not know what “Holi” is. Even if they do know, if you cannot use the words “India,” “Hinduism,” or “festival,” they might be able to guess that it is the name of a festival in some country, but it is uncertain whether they can arrive at “Holi.”

In this way, you can understand that “it is difficult to convey only the nature of things and restore information 100% completely.”

The same applies to “communication” in IUT. Even if you communicate the “symmetry” of something, it is not necessarily restored 100% accurately. In fact, there is a higher possibility that “distortion” will occur during the process of communication, and it may not be restored correctly.

That’s why professor Mochizuki thought about whether it is possible to formalize the “distortion” during communication.

The claims that this formulation is possible is the IUT and the inequality that shows the “distortion” is listed in “宇宙と宇宙”. And it goes on to say that this inequality may hold the key to the proof of the “abc conjecture.

In “宇宙と宇宙,” this is how the IUT is explained. If you read this article, you should be able to follow the flow, albeit roughly. If you read the book, you should be able to understand it more thoroughly, so please pick it up if you have the chance.

Now let’s move on to the “abc conjecture,” which is not touched on much in “宇宙と宇宙,” based on the “abc予想入門.”

What is an abc Conjecture?

How abc Conjecture was Born

Before delving into the abc conjecture itself, let’s first take a look at how it came about.

In the following text, two terms “integer” and “polynomial” are involved. You probably don’t need an explanation for “integer,” but let me explain “polynomial.” Simply put, it refers to an equation with multiple terms, such as “x+1” or “3a+2b+c.”

It has been known in mathematics for a long time that there is a relationship between “integer” and “polynomial.” The theories that hold true in the world of “integers” also hold true in the world of “polynomials,” or vice versa. For example, there exist “polynomial” versions of the very important unsolved problems in the field of “number theory,” which deals with “integers,” such as the “Riemann hypothesis” and the “Langlands program,” and they have already been proven.

Given this relationship, it would be natural to think about applying the theories that work for “integers” to “polynomials” and vice versa.

In fact, there has long been something called the “polynomial version of the abc conjecture” in the mathematical world, and it was proven quite early on. So it’s natural to wonder if the same thing holds true in the world of “integers.”

And that’s how the “abc conjecture” was born.

What is the abc Conjecture?

Now, let’s delve into the details of the abc conjecture.

First, let’s talk about the “conjecture that actually proved incorrect” (referred to as “abc conjecture (hope)” in the ” abc予想入門”).

First, let’s explain the meaning of this formula.

“Coprime” means that two or more integers have no common factors except for 1. For example, “a=2, b=3, c=5” are coprime because they have no common factor except 1. However, “a=4, b=6, c=10” are not coprime because they have a common factor of 2. If we divide them by 2, we get “a=2, b=3, c=5”, and they become coprime.

Next, “max{|a|,|b|,|c|}” means the largest absolute value among a, b, and c. The symbol “||” represents the absolute value, which means like we treat negative numbers as positive.

Let me explain with some examples (ignoring the condition that a+b=c).

Let’s say we have “a=7, b=-25, c=10”. If we just pick the largest number without considering its absolute value, then “c=10” would be the answer. However, when we consider the absolute value, which means we treat negative numbers as positive ones, the number with the largest absolute value in this case is “b=-25”.

Now, let’s talk about “rad(abc)”. It means “the product of the prime factors of a, b, and c”, but it might be hard to understand without an example.

For example, let’s say “a=6, b=12, c=3”. If we factorize each number into prime factors, we get “a=2×3”, “b=2×2×3”, and “c=3”. The prime factors used in these three numbers are only “2” and “3”. Therefore, rad(abc) is the product of these prime factors, which is 2×3=6.

Let’s look at another example. Suppose we have “a=7, b=30, c=11”. The prime factorization of these numbers are “a=7”, “b=2×3×5”, and “c=11”. The prime factors used here are “2”, “3”, “5”, “7”, and “11”. Therefore, rad(abc)=2310.

Now, you may understand the meaning of the “abc conjecture (hope)” mentioned earlier.

However, this has been proven not to be correct. Mathematicians then came up with a “probably correct conjecture.” This is generally known as the “strong abc conjecture” and is denoted as “abc conjecture (☆)” in “abc予想入門”.

The difference from earlier is the “^2” part. This is the notation “squared,” meaning that rad(abc) is squared, so (rad(abc))^2=36 for “a=6,b=12,c=3” and (rad(abc))^2=5336100 for “a=7,b=30,c=11”.

Now, it’s thought that this is probably correct, but it hasn’t been proven yet. Also, in fact, what Professor Mochizuki claims to have proven through IUT is not the “abc conjecture(☆).” The author express the conjecture that Professor Mochizuki claims to have proven as “abc conjecture(Professor Mochizuki)” in this book, it looks like this:

And this “abc conjecture(Professor Mochizuki)” is what is generally known as the “abc conjecture.”

The symbol “^(1+ε)” means to raise rad(abc) to the power of (1+ε), just like earlier. It might be harder to understand, but you may understand that if we set “ε=1” and “K(ε)=1”, it becomes the same as the “abc conjecture(☆)”.

There are several types of things called the “abc conjecture”, and it’s important to understand that what Professor Mochizuki claims to have proven is just one of them.

Relationship with Fermat’s Last Theorem

When it was a hot topic that the “abc conjecture might have been proven,” it was also a hot topic that “if the abc conjecture is proven, Fermat’s Last Theorem can be proven in 10 lines.” However, even if “the abc conjecture is proven to be true by IUT,” “it is not possible to prove Fermat’s Last Theorem in 10 lines.”

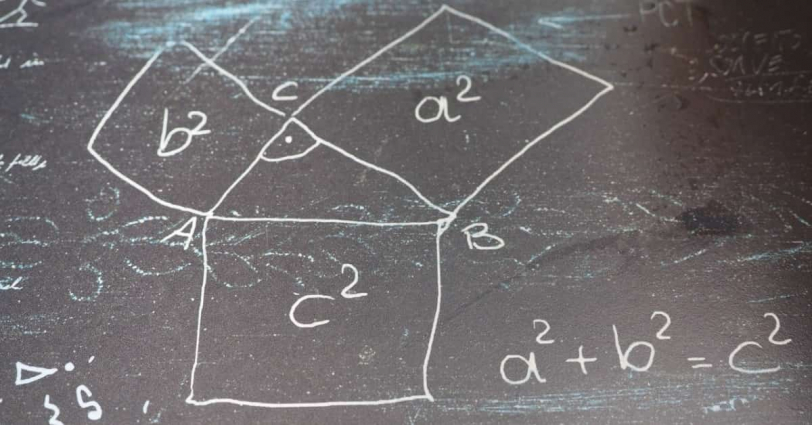
Let’s explain this area and end this article.

When I say “if the abc conjecture is proven, Fermat’s Last Theorem can be proven in 10 lines,” the “abc conjecture” I refer to is called the “strong abc conjecture,” written as “abc conjecture(☆)” in this article. As we confirmed earlier, this is different from the “abc conjecture (Professor Mochizuki)” that Professor Mochizuki claims to have proven.

Furthermore even if “abc conjecture (Professor Mochizuki)” is proven to be correct, it does not confirm whether “abc conjecture (☆)” is also correct. Why is that?

As explained earlier, “abc conjecture (☆)” is the expression of the case “ε=1 and K(ε)=1” in “abc conjecture (Professor Mochizuki).” In other words, even if “abc conjecture (Professor Mochizuki)” is proven to be correct, it does not necessarily mean that “abc conjecture (☆)” is correct unless it is proven that “ε=1 and K(ε)=1” is also true.

However, Professor Mochizuki has not shown that “K(ε)=1” when “ε=1” in his paper, and provided a clear value for K(ε) in the first place.

In other words, it means that even if “abc conjecture (Professor Mochizuki)” is proven to be true, it does not necessarily mean that “abc conjecture (☆)” is also true, and “Fermat’s Last Theorem” cannot be proven in 10 lines.

The statement “If abc conjecture is proven, Fermat’s Last Theorem can be proven in 10 lines” is impressive and often appears when searching on the internet, but it is important to be accurate to avoid misunderstandings.

And in both “宇宙と宇宙” and “abc予想入門”, there is not much detail provided (and of course, I don’t understand it either), but it’s said that by using the inequalities derived from IUT, we can prove that “abc conjecture (Professor Mochizuki)” is correct.

Conclusion

This book is a “work that makes us feel like we vaguely understand” about “IUT (Inter-Universal Teichmüller Theory)”, which caused shock, controversy, and perhaps resignation in the world of mathematics and “abc conjecture”, which was seems to be proven by IUT. While “abc予想入門” is honestly quite difficult and not necessarily recommended, “宇宙と宇宙をつなぐ数学” is a work that I think you can follow along with if you try hard enough, so please give it a read (Neither of which seems to have been translated into English as of yet though).

It’s exciting to think that a theory that could revolutionize the math world was born in Japan, isn’t it.