What is Galois Theory and How it Changed Mathematics Forever

I wrote this article in Japanese and translated it into English using ChatGPT. I also used ChatGPT to create the English article title. I did my best to correct any translation mistakes, but please let me know if you find any errors. By the way, I did not use ChatGPT when writing the Japanese article. The entire article was written from scratch by me, Saikawa Goto.

Introduction

Movies and books covered in this article

Three takeaways from this article

Self-introduction article

The quotes in the article were translated using ChatGPT from Japanese books, and are not direct quotes from the foreign language original books, even if they exist.

About the Setting of Math Girls

First, let’s introduce the setting of this series of math books, which is aimed at the general public. Although it is a math book, it is structured like a story, so we can enjoy the human relationships and romantic developments of the characters.

The protagonist is the “narrator” (The protagonist does not have a name.), a third-year high school student who loves math. In addition to his school classes and exam preparation, he conducts personal research on topics that interest him.

Around him, there are various types of “Math Girls.”

Miruka-san, who is the same age as the narrator, is a math genius and a guiding figure for math enthusiasts centered around the narrator. With her overwhelming mathematical talent that is hard to believe coming from a high school student, she leads everyone into unknown worlds.

Tetra-chan is a junior who is one grade lower than the narrator. At first, she came to learn from the narrator because she was not good at math, and she was not particularly strong in math. However, through interactions with the narrator and Miruka-san, she steadily gained strength in math. She sometimes comes up with ideas and understandings that even the narrator did not think of. Her strength lies in her sensitivity to words and not leaving any unclear parts behind.

Yuri is the narrator’s cousin and is in the third year of junior high school. She often comes to the narrator’s room to learn math. She cannot understand difficult math problems because she is in junior high school, but she is interested in math. She is extremely strong in “logic” and sometimes surprises the narrator.

Lisa is the “master” of Narabikura Library and has distinctive red hair. She is a woman of few words and mostly communicates by speaking a single word, but her mathematical talent is truly remarkable. This is because she is the cousin of Miruka-san. She is always tinkering with her laptop computer.

The story is about how these individuals delve deeper into the world of mathematics through various discussions.

In the “Math Girls” series, all except the first book have subtitles, which serve as the “final destination” of the work. This time it’s “Galois theory.” In this book, the story ultimately follows Galois’s first paper, which is presented as an exhibition at the school festival.

Here’s How “Galois Theory” is Depicted in “Math Girls”

Who is Galois?

Before I introduce the contents of this book, let’s first summarize the genius mathematician, Galois.

He is sometimes called “the genius in the history of mathematics” because he single-handedly created a field that did not exist in the world of mathematics until then. Moreover, he accomplished this at the young age of just 20 years old. He was so ahead of his time that his contemporaries had a hard time understanding him, which shows just how innovative he was.

Furthermore, there is a legendary episode that surrounds Galois. He died at the young age of 20 in a duel. Great historical figures are known for their various causes of death, but it would be astonished to die in a “duel.”

Galois was not born and raised in a blessed environment but displayed exceptional talent and achieved great mathematical feats, yet he was not understood by anyone. Afterwards, he fought a duel for his beliefs and lost, and it was only after his friend, who had no mathematical knowledge, continued to have Galois’ papers read by various mathematicians that his work was finally recognized. Galois is known for such dramatic life, filled with hardship and triumph.

Now, I have completely forgotten where I saw this, but I remember reading an argument about “Galois’s genius” in comparison to Einstein. Let me try to summarize it based on my memory.

Certainly, in both mathematics and science, it is common for multiple individuals to come up with similar ideas at the same time, and often “who stood out from the crowd” is evaluated. Alternatively, there are cases where the person who first solves a known problem, task, or conjecture is evaluated.

However, Galois created something completely new and innovative when almost no one had the same problem awareness, so it can only be said that it was tremendous.

That’s why Galois’ first paper is said to be extremely difficult. According to this book, even Poisson, who is considered the greatest mathematician of Galois’ time, said it was “difficult to read.”

But that’s understandable, because he created a completely new field and had to explain unfamiliar concepts using the “terms” of existing mathematics.

Let me explain this with an example of “creating a smartphone in the Edo period (Japan, 400 years ago)”. Of course, at that time, words like “screenshot” or “app” didn’t exist, and even the concept of “making a phone call” didn’t exist. It would be extremely difficult to explain what a smartphone is using only the words that existed in the Edo period.

Galois was in a similar situation. Regarding the theory that Galois created, there are now words like “group” and “field” that explain the necessary concepts. However, Galois had to explain those concepts using only existing mathematical terms, without words like “group” or “field” existing at the time.

In that sense, it’s impressive that Galois’ achievements have survived to this day. Galois died at the young age of 20, and his best friend who was entrusted with his papers didn’t have much mathematical knowledge. Despite that, there were people who tried to deliver and understand the concepts that even the top mathematicians of the time couldn’t grasp, and it’s thanks to them that Galois theory has been preserved.

Moreover, the field that Galois created is recognized as essential in modern mathematics. The concept of “symmetry” is important not only in science but also in mathematics, and the grammar for describing this “symmetry” is “Galois theory”. In other words, it can be said that without “Galois theory”, it would have been impossible to describe “symmetry”. In that case, it’s highly possible that research in science and mathematics would have been greatly hindered.

Now, the “final destination” of this book is the “Galois theory”, but I didn’t feel it was as difficult as I had anticipated (though of course it is very challenging). In this article, I won’t go into the details of Galois theory itself (as I haven’t fully understood it), but by following the flow of the book from the beginning to the end, I think you can get a sense of what Galois was thinking and feel like you “understand it”.

From “Amidakuji” and “Quadratic Equation” to the Discussion of “Field” and “Group”

In this book, the well-known game of “Amidakuji (a decision-making method unique to Asian countries)” appears as a relatively important item. It may be difficult to understand how to mathematically think about “Amidakuji,” but the narrator and “Yuri” in this book explore what kind of structure “Amidakuji” has using various symbols and unique notations such as “Gururin” and “Suton”.

Then, the discussion expands from quadratic equations to the concept of “field.” This “field” becomes important throughout the entire book, so it’s important to understand it well when reading the book. However, I must say that this “field” is quite challenging to grasp.

“Field” is a “set of numbers for which addition, subtraction, multiplication and division are defined.” In other words, it means “addition, subtraction, multiplication and division are possible” and “the result of the calculation will be the same set.”

It might be hard to understand, so let’s take “real numbers” as an example. “Real numbers” include all regular numbers, including those with decimal points and square roots (but not complex numbers). (Although “regular numbers” isn’t a precise term in math, can you understand it roughly?)

Now, when we add, subtract, multiply, or divide two real numbers, the answer will always be another real number. That’s why we can say that the set of real numbers is “field.”

On the other hand, what about “integers”? If the result is always an integer when we add, subtract, multiply, or divide between integers, we can call it “field.” Unfortunately, the “set of integers” is not “field” because the result of the calculation between integers, such as “3÷2＝1.5,” can be a number that is not an integer.

Thus, the set that allows addition, subtraction, multiplication and division (defined) and has results that belong to the same set is called “field.”

Then, the discussion moves on to the topic of “group” using an example of “Amidakuji.” This “group” is even more complicated than the “field.” Unlike the “field,” it cannot be explained in an easily understandable way, so I will omit it.

Just for example, the explanation using the “Amidakuji” is a type of “group” called the “symmetric group,” but it roughly refers to the “operation that does not change even if replaced.” Through the example of “Amidakuji,” the “symmetric group” is explained, and then the definition of the entire “group” is given, followed by an introduction to various types of “group.”

After that, Mr. Muraki, a prominent character in the “Math Girls” series, appears with a card. He is the math teacher at the high school where they all attend, and he hands short descriptions on a card to the narrator and Tetra-chan to research. This time, the card only had the formula “x^12-1” (meaning “x to the power of 12 minus 1”).

From this, they conduct their own research and delve into learning about regular dodecagon and trigonometric functions. Then Miruka-san appears and takes them to even greater heights, introducing concepts like “primitive 12th root of unity,” “cyclotomic polynomial,” and “conjugate complex number” that the narrator and Tetra-chan couldn’t have reached on their own.

“Angle Trisection” and “Cubic Equation’s Formula for Solutions”

“Field” and “group” are mostly conceptual topics, and as someone who’s not good at such topics, I found it hard to keep up.

However, this book also has calculation-driven parts, and I quite enjoyed those parts.

That’s the story of “angle trisection” and “cubic equation formula for solutions.”

Let’s start with “angle trisection.” This problem is a famous one that has been known since ancient Greece, and many mathematicians have tried to solve it.

“Angle trisection” is a problem that asks whether a given angle can be divided into three equal parts using only a “straightedge to draw a line through two given points,” and a “compass to draw a circle with one given point as the center and passing through the other given point.” This means that the problem asks if it’s possible to divide an angle into three equal parts without using tools like a protractor to measure angles directly.

However, the problem of “angle trisection” has already been solved, and it’s known that there are some angles that cannot be trisected using only a straightedge and compass.

Now, in this book, we will transform “angle trisection” from a “geometry problem” to a “calculation problem.” What does this mean?

In fact, it is known that we can perform “addition, subtraction, multiplication and division” and “extraction of square root” using only “straightedge” and “compass”. So, “angle trisection” is a problem of “whether a given angle can be divided into three equal parts by using only addition, subtraction, multiplication and division, and extraction of square root”. And the numbers that can be created using “addition, subtraction, multiplication and division, and extraction of square root” are called “Constructible number”.

So, the problem of “whether a certain angle can be trisected” can be rephrased as “whether that angle is a Constructible number”, and furthermore, it can be reduced to the problem of “whether a certain equation has a solution that is a Constructible number”. Moreover, by incorporating the concept of “field”, the discussion goes on to “grasping angle trisection as a solution to the equation”.

It’s quite difficult, isn’t it? If you actually read the description in this book, you may be able to understand what they are talking about.

I had some fragmented knowledge about “angle trisection” before reading this book, but I didn’t know that a geometric problem could be seen as a problem of finding the solution to an equation, including the story that “it is possible to draw a regular 17-sided polygon” shown by Gauss. I found it very interesting to read.

As we approach the “final destination” of “Galois theory,” the topics that come up become increasingly difficult, with discussions on “vectors” and “cubic equations.” While these terms may be familiar from high school classes, it doesn’t mean that the discussion will be easy.

In particular, when it comes to the “cubic equation,” there’s talk of something called the “Lagrange resolvent” that I have not heard of before.

This is related to Mr. Muraki’s card problem, where by following his seven cards in order, they can derive the “formula for solutions of the cubic equation,” and then by considering the “Lagrange resolvent,” they can understand what it means to “algebraically solve an nth-degree equation.”

But what does it even mean to “algebraically solve an equation?” Well, you’ll just have to read the book for that. It’s really interesting, but understanding it well enough to explain to someone else can be pretty difficult.

Now, moving on from there, there’s a rare scene where Tetra-chan gives a lecture to the narrator, and finally the story heads towards “Galois theory”. As mentioned at the beginning, the description of “preparing for and exhibiting at the school festival” leads into the explanation of “Galois theory”.

About Galois Theory

This article doesn’t delve too deeply into the subject matter, but I’ll roughly follow the description of “Galois theory” in this book.

First, as part of the exhibition preparation, Yuri introduces her research on “Amidakuji” once again. She first classifies something called “3rd symmetric group S3,” divides it into “subgroups of S3,” and then names the resulting set of groups “residue class.” And the story unfolds with the classification of “symmetric group” based on this “residue class.”

Furthermore, the set of “residue class” becomes “group,” which is treated specially as “normal subgroup.” And it’s also shown that this “normal subgroup” is one of the key concepts in “Galois theory.”

Even if you are told that, it’s difficult to understand, right…? Well, in this article, I cannot explain all the content, and since I don’t fully understand it myself, it will inevitably be an insufficient introduction. I think you can understand it a little better if you read this book, so please give it a try.

Finally, for the school festival exhibition, this book will delve into Galois’ first paper, which he entrusted to his best friend on his deathbed. It will carefully explore what ideas are contained in this first paper, which is full of Galois’ thoughts. While following this flow, the book leads us to the subject of “Galois theory”.

Finally, let’s briefly touch on how Galois himself arrived at “Galois theory”.

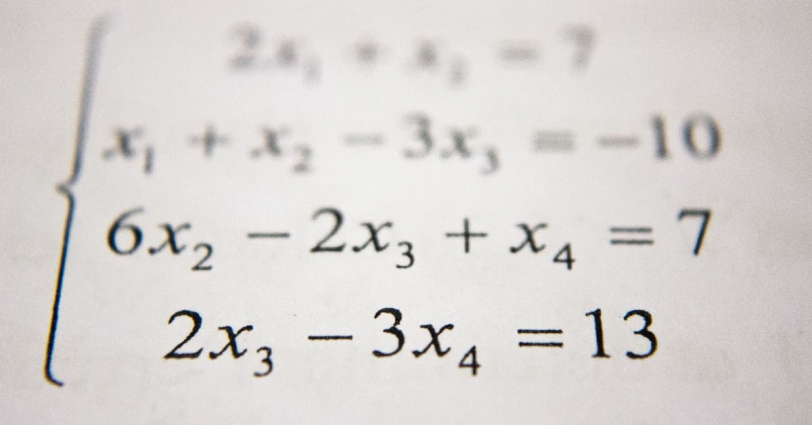
During Galois’ time, finding the “formula for solutions” was highly valued in mathematics. Mathematicians had already found the formula for solutions up to quartic equations through their struggles, but no one could come up with the quintic formula no matter how hard they tried.

At that time, there was a mathematician named Abel who radically changed the way the problem was approached and proved that “there is no formula for solutions for the quintic equation.” In a way, he can be seen as someone who shared the same direction as Galois but couldn’t become Galois.

Now, it is said that Galois never had the opportunity to learn about Abel’s work during his lifetime (Abel’s achievements, like Galois’, took a long time to be recognized). So what was Galois thinking? It was “what is the necessary and sufficient condition to algebraically solve any equation?” Roughly speaking, it would be like “under what conditions does an nth-degree equation have a formula for solutions?”

And from such an idea that no one else had thought of, he came up with “group theory (= Galois theory)”.

My Thoughts on This Book

That’s all for the mathematical descriptions in this article. From here, I will write my thoughts on the work “Math Girls.”

This book is the fifth in the series, and the level of difficulty is gradually increasing. Of course, it depends on the “final destination” (if the difficulty level of the “final destination” is high, the difficulty level of the entire work will also increase), but I also feel that Tetra-chan’s understanding has improved considerably, which is one of the reasons.

At first, Tetra-chan came to learn from the narrator because she was not good at math, but through interactions with the narrator and Miruka-san, she has leveled up quite a bit, and the parts with Tetra-chan are now quite challenging.

However, this book is still very well done, and the narrator’s cousin Yuri is in a beginner’s position that is quite sympathetic to the reader, so I feel that the overall balance is good.

Also, although this book is a mathematical book that unfolds like a story, the story is not just an extra. The mathematical part and the story part are very organically intertwined, and it feels very skillful. Changes in human relationships that echo the mathematical development are also depicted, and the balance is remarkable.

Conclusion

As the series progresses, the content becomes quite challenging for those who are more inclined towards liberal arts, but I believe that the first volume is quite easy to read. Don’t be intimidated by the descriptions in this article, and start by reading the first volume.