Simon Singh’s “Fermat’s Last Theorem”: A Mathematical Drama

I wrote this article in Japanese and translated it into English using ChatGPT. I also used ChatGPT to create the English article title. I did my best to correct any translation mistakes, but please let me know if you find any errors. By the way, I did not use ChatGPT when writing the Japanese article. The entire article was written from scratch by me, Saikawa Goto.

Introduction

Movies and books covered in this article

I will write an article about this movie/book

Three takeaways from this article

Even if you’re not good at math, I only recommend reading Simon Singh’s “Fermat’s Last Theorem.”

Self-introduction article

Please refer to the self-introduction article above to learn about the person writing this article. Be sure to check out the Kindle book linked below as well.

The quotes in the article were translated using ChatGPT from Japanese books, and are not direct quotes from the foreign language original books, even if they exist.

Introducing Two Recommended Books for Those Who Want to Learn About “Fermat’s Last Theorem”

Simon Singh’s “Fermat’s Last Theorem” and Yuki Hiroshi’s “Math Girls: Fermat’s Last Theorem” are Both Easy to Understand and Highly Recommended

In this article, I will introduce the two books mentioned in the headline. While I will touch upon “Fermat’s Last Theorem” itself, to be honest, this “proof story” filled with a grand drama and profound knowledge is not easy to explain. I definitely want you to read the books and experience its interesting and shocking aspects for yourself.

Let me write about the difference between the two books. Both works deal with “Fermat’s Last Theorem” head-on, but they have slightly different characteristics. Simon Singh’s book focuses more on the “human drama” aspect, while “Math Girls” emphasizes the mathematical descriptions.

Both of these books are math books for general audiences that even humanities majors can enjoy (“Math Girls” gets more difficult as you get to the latter half of the series though). If you want to learn more about “Fermat’s Last Theorem,” including what kind of problem it is, what kind of history it has, and what kind of mathematical knowledge was utilized in the process of proving it, I highly recommend reading both of these books.

In particular, if you’re “someone who is interested in math but has no knowledge of it and isn’t confident that you can finish reading a whole book,” I recommend Simon Singh’s book. His “Fermat’s Last Theorem” is so easy to read and breaks things down so well that we’ll feel like it’s a waste not to read it just because you’re not good at math.

Simon Singh’s book “Fermat’s Last Theorem” is a work that has a lot of human drama, but also has a substantial amount of mathematical description. In other words, it doesn’t assume that the readers won’t understand it, and it’s also not written in a way like “they wouldn’t understand anyway.”

For example, in “Fermat’s Last Theorem,” the term “modular form” appears. Even I, who have studied math, cannot explain exactly what it is, and it is a term that you wouldn’t encounter unless you have properly studied mathematics.

And usually, books that include such advanced words are written by mathematicians, which can make the descriptions difficult. To put it poorly, but I sometimes encounter descriptions that make me “feel” as if the writer is thinking, “Most readers will not understand the ‘modular form’ anyway.

However, Simon Singh takes on the challenge of explaining difficult words and concepts without avoiding them. Of course, whether the explanation is successful or not depends on the reader (I personally think it’s successful), but at least there is no impression that “it won’t be understood anyway.” He explains in a way that is understandable to ordinary people, even though it may be difficult.

And the reason why Simon Singh can do would be that he is not a mathematician. He originally worked for the BBC in the UK, and ended up writing this book after featuring “Fermat’s Last Theorem” in a program. Simon Singh’s “Fermat’s Last Theorem” is highly regarded as one of the best popular science and math books.

I hope you will pick it up.

What is “Fermat’s Last Theorem”?

In this article, let’s briefly touch on what “Fermat’s Last Theorem” is.

First, let’s talk about the strangeness of the name.

“Fermat’s Last Theorem” was proven by Andrew Wiles in 1995, but it had been an unsolved problem for a long time since the mathematician Fermat (who was actually a judge by profession) left it in the 1600s.

In mathematics, the word “theorem” means “proven”. However, “Fermat’s Last Theorem” was called a theorem even before it was proven in 1995. In addition, it even has the word “Last” in it. The theorem/forecast with the word “Last” would be probably only “Fermat’s Last Theorem” In the mathematical world.

So why is it called that way?

To explain this, I need to first talk about Fermat. He was a person who conducted research in mathematics as a hobby alongside his job. He used to send letters to top mathematicians of his time, challenging them with statements like “I have proven this problem, can you do it too?”, which made him quite an unpleasant character.

Fermat was such a person, so many of hypothesis were not written down “how I proved it”. After Fermat died, his son organized his father’s research and announced “48 problems for which my father said he had proofs, but the proofs were not.”

Mathematicians tackled these 48 problems, some of which took years to solve, but through their efforts, it was eventually determined that 47 out of the 48 problems were “all correct, just as Fermat claimed.”

At last, there remained what is now called “Fermat’s Last Theorem.” In other word, the word “Last” means “the one that remained last out of the 48.”

Furthermore, as previously mentioned, out of the 48 problems Fermat left, all 47 of them were proven to be correct. Therefore, it is likely that this one that remained at the end is also correct. Based on that understanding, it came to be called a “theorem” even before it was proven.

Fermat’s 48 problems were written in the margins of the ancient Greek mathematician Diophantine’s book “Arithmetica.” Fermat probably wrote down his ideas while reading “Arithmetica.” And in the margin notes that would later be called “Fermat’s Last Theorem,” there is a famous quote written.

I have discovered a truly marvelous proof of this, which this margin is too narrow to contain.

Simon Singh, “Fermat’s Last Theorem”

In reality, “Fermat’s Last Theorem” was indeed correct, but it is now believed that Fermat himself could not prove it. This is because Andrew Wiles’ proof includes mathematical knowledge that did not exist in Fermat’s time. The prevailing theory is that Fermat probably just misunderstood and thought he had proved it.

So, let’s talk about “Fermat’s Last Theorem” itself.

I want you to remember the “Pythagorean theorem” that you should have learned in your student days.

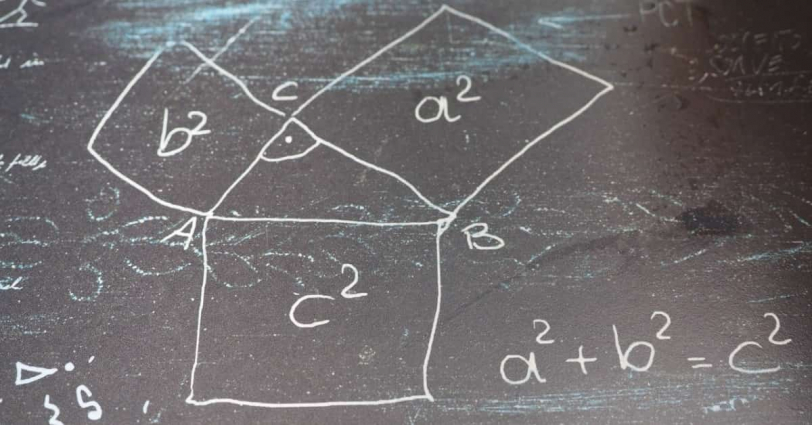
It goes like this: (x^2) + (y^2) = (z^2) (* the symbol ^ means “to the power of”). For example, (x=3, y=4, z=5) satisfies this equation (try calculating it yourself). By choosing the right numbers for x, y, and z, you can find combinations that make this equation true.

Then, how about changing the “squared” part to something else? In other words, when you increase the number of “power” like this:

(x^3) + (y^3) = (z^3)
(x^4) + (y^4) = (z^4)
(x^ 5) + (y^5) = (z^5)
…

Thus, the question is whether there exists a combination of x, y, and z that makes the equation valid as in the “Pythagorean theorem” when the number of “power” is increased.

And Fermat disagreed with this idea and claimed that “there are no combinations of x, y, and z that satisfy the equation for powers of 3 or higher.” This became known as “Fermat’s Last Theorem.”

Mathematically, it can be written as follows:

For natural numbers n greater than or equal to 3, there are no solutions to the equation (x^n) + (y^n) = (z^n) (where x, y, and z are also natural numbers.)

The remarkable thing about “Fermat’s Last Theorem” is that the problem itself is understandable to anyone. You should be able to understand what the problem is saying. That’s why many amateur mathematicians also attempted to prove “Fermat’s Last Theorem.”

However, it is extremely difficult to solve, which is why it had remained unsolved for over 350 years, as “the Holy Grail of mathematics,” and the stories of the people involved in this proof are quite dramatic.

In “Math Girls,” How is “Fermat’s Last Theorem” Discussed?

“Math Girls” is a novel-like work in which high school boys and girls grow through mathematics, and it is a work that allows us to learn about mathematics thoroughly. Please read the following article for information on the story’s settings, etc.

In the “Math Girls” series, the subtitle of the book is set as the “final destination” of the entire work, and various mathematical descriptions that may not seem connected come together as an explanation of the “final destination.” Rather than starting with “Fermat’s Last Theorem” right away, the book takes a step-by-step approach like climbing a staircase, aiming for the “final destination” while acquiring the necessary knowledge and logic. This makes it very easy to understand and ensures that the readers don’t get left behind (although there are still some parts that may be difficult to follow, especially with descriptions that are quite challenging).

In “Math Girls: Fermat’s Last Theorem,” various prior knowledge is explained, including concepts related to the foundation of mathematics such as “group” and “field,” the concept of “mod,” which is the “remainder when divided by a certain number,” and new knowledge that I learned for the first time in this book like “primitive Pythagorean triple.”

The structure of “Math Girls: Fermat’s Last Theorem” is great because it provides clear steps needed to understand the proof of Fermat’s Last Theorem. If you work hard to understand each description, you can reach the theorem. The story is also engaging as it progresses in a narrative format. Although there are many formulas, which may make it challenging for those who struggle with math, if you persevere, you should be able to read properly. I encourage you to give it a try.

The Relationship Between “Taniyama-Shimura Conjecture” that Completely Transformed the Treatment of “Fermat’s Last Theorem”

Nowadays, “Fermat’s Last Theorem” is treated like “the Holy Grail,” and Andrew Wiles, who proved it, is praised for his achievement. However, at one point in time, “Fermat’s Last Theorem” was treated as a “problem that was not worth proving.”

Why was it considered so?

For example, there is a difficult problem in mathematics that has yet to be proven called the “Riemann hypothesis”. Although this article does not explain the details of this hypothesis, it is considered “what every mathematician is waiting for a proof”. It means that if it is not proven to be true, it will hinder progress and cause problems in many fields.

However, the “Fermat’s Last Theorem” was not such problem in the past. It was a very famous problem, so they might get a sense of accomplishment when they solve it. But even if the “Fermat’s Last Theorem” was proven, there would have been no other achievements beyond “proving Fermat’s Last Theorem”. In other words, it was not thought to have a ripple effect on other fields just by proving it.

Furthermore, “Fermat’s Last Theorem” has been a difficult problem that has challenged many mathematicians for years. If they were to try to solve it, they could end up devoting their entire life to it without making any progress and end their life with no achievements as a mathematician.

Nobody would want to live that life. That’s why many people started thinking it would be best not to even try to solve “Fermat’s Last Theorem”. Well, I think that’s a natural decision.

However, one day, a mathematician named Frey made a shocking announcement. He claimed to have proven the following fact:

If the Taniyama-Shimura conjecture is true, then Fermat’s Last Theorem is also true.

As soon as this became known, “Fermat’s Last Theorem” was once again in the spotlight. This is because the “Taniyama-Shimura conjecture” was also a very important problem in the field of mathematics, eagerly awaited for its proof by many mathematicians.

Until now, it was thought that even if “Fermat’s Last Theorem” was proven, there would be no other significance than the fact of “having proven it”. However, it was realized that if the “Taniyama-Shimura conjecture” was proven, “Fermat’s Last Theorem” would come along as a bonus. Although the “Taniyama-Shimura conjecture” is also an extremely difficult problem, it would be worth challenging it if “Fermat’s Last Theorem” can incidentally be solved as an added bonus.

I don’t know if they thought that way, but it seems that this kind of atmosphere had come to surround the world of mathematics. And mathematicians had become working hard to prove the “Taniyama-Shimura conjecture”.

(As a side note, it’s important to understand that the claim “If Fermat’s Last Theorem is proven, then Taniyama-Shimura conjecture is also true” is not correct. The correct claim is that “If Taniyama-Shimura conjecture is proven, then Fermat’s Last Theorem is also true”.)

So, what exactly is the “Taniyama-Shimura conjecture”? It is a hypothesis proposed by Japanese mathematicians.

This involves two completely different fields: “Elliptic curve” and “Modular form”.

“Elliptic curve” is a classical field of mathematics that has been studied by ancient mathematicians for a long time. “Fermat’s Last Theorem” can also be said to be a problem in the “Elliptic curve” genre. On the other hand, “Modular form” is a relatively new and mathematically isolated field with little connection to other fields. Although there are researchers, it is a field that can be said to have been left behind in mathematics as a whole.

And the “Taniyama-Shimura conjecture” connects these two fields by proposing that a specific “Modular form” corresponded to “a specific Elliptic curve”.

Let’s consider this using the alphabet as an example. Each uppercase and lowercase letter corresponds to one another, like “A” and “a,” or “M” and “m.” It’s not like “B” corresponds to both “b” and “c,” or that there’s no corresponding lowercase letter for “Q.”

Similarly, the conjecture suggests that if they choose a certain Elliptic curve, there exists only one corresponding Modular form.

The ground-breaking of this conjecture is that even if there’s a problem that can’t be solved in the field of Elliptic curves, it might be solvable by converting it to a Modular form. This idea excited mathematicians all over the world.

And with that revolutionary idea further linked to “Fermat’s Last Theorem,” it’s no wonder mathematicians were excited.

Wiles’ Proof and Iwasawa Theory

Now, at this point, we can say that we are ready. It was just a remaining matter of “who would prove the Taniyama-Shimura conjecture,” and the person who achieved that was Andrew Wiles.

When Wiles was just 10 years old, he encountered “Fermat’s Last Theorem” and became determined to prove it, which is a very dramatic story. However, he received advice to stay away from “Fermat’s Last Theorem” and was warned that if he couldn’t prove it, he wouldn’t have any achievements as a mathematician. So, he decided to pursue a different research topic while suppressing his own desire.

The subject he chose to study was called “Iwasawa theory,” which is another theory created by a Japanese mathematician. He became renowned as an expert in “Iwasawa theory.”

Afterwards, Wiles began working on his childhood dream of proving “Fermat’s Last Theorem”, but he didn’t tell anyone except his wife about it. His attitude was seen as unusual, as mathematicians usually deepen their thinking by discussing their current research with other mathematicians. It seems that he didn’t have contact with other mathematicians and didn’t even talk about what he was researching, but worked tirelessly in the attic.

Then one day, Wiles presented his theory to a group of mathematicians. Although they didn’t know what he was researching, as his theory was explained, they became convinced it was about “Fermat’s Last Theorem” and when he announced “proof completed”, they were filled with excitement.

However, this was the beginning of Wiles’ agony.

In both mathematics and science, published papers go through a process called “peer review,” in which they are evaluated by other scholars. And during this peer review, a fatal flaw was found in Wiles’ proof.

The person who could fill this gap, which Wiles could not, would be recognized as the “one who proved Fermat’s Last Theorem.” While Wiles had been studying alone and had completed most of the proof by himself, if he didn’t solve this last remaining problem, someone else would be recognized as the one who finally pluged the hole.

Wiles was backed into a corner. He couldn’t think of anything. He was about to give up… that was the moment he had an inspiration.

He thought that “Iwasawa theory” might be applicable. What a surprise, the “Iwasawa theory,” in which he was renowned as an expert, was the key piece to plug the last hole in Wiles’ proof.

And thus, the proof of “Fermat’s Last Theorem” was completed. Naturally, Wiles received praise from all over the world, but he could not win the “Fields Medal,” which is said to be the highest award in the field of mathematics, because there is an age limit of 40 or younger. I’ve heard that it’s because “important mathematical work can only be done when they’re young.” However, instead of giving him the “Fields Medal,” the International Mathematical Union gave Wiles a special commendation.

Even looking only at Wiles, who gave the final proof, this story is packed with drama. When you consider all the mathematicians who were directly or indirectly involved in “Fermat’s Last Theorem,” it is a very attractive story with a human drama that is far beyond the world of mathematics.

Conclusion

When it comes to math, it’s often thought of as “boring.” However, the drama created by those who seriously engage with math is anything but “boring.”

Whether it’s Simon Singh or “Math Girls,” difficult math descriptions may come up, but if you don’t understand something, you can just skip it. I definitely want you to experience how many people have struggled with math.